
 =
=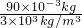 =0.3×10-4m3
=0.3×10-4m3 +VA)=G甲+GA
+VA)=G甲+GA +0.3×10-4m3)=3.4N+0.9N
+0.3×10-4m3)=3.4N+0.9N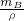 +
+ )=3.4N+mB×10N/kg+mC×10N/kg
)=3.4N+mB×10N/kg+mC×10N/kg +
+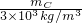 )=0.34kg+1.5mC+mC
)=0.34kg+1.5mC+mC -2V排′=8.0×10-4m3+
-2V排′=8.0×10-4m3+ -2×3.4×10-4m3=5.2×10-4m3
-2×3.4×10-4m3=5.2×10-4m3 =0.013m
=0.013m

科目:初中物理 來源: 題型:

查看答案和解析>>
科目:初中物理 來源: 題型:閱讀理解
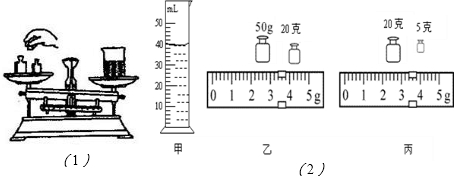
| 量筒中海水的體積 V/cm3 |
玻璃杯和海水的質量 m1/g |
剩余海水與玻璃杯的質量 m2/g |
海水的密度 ρ/㎏?m-3 |
40 40 |
73.4 73.4 |
28.4 28.4 |
1.125×103 1.125×103 |

| 液體種類 | 酒精 | 水 | 可樂 | 醬油 |
| 彈簧秤的示數(N) | 2.6 | 2.8 | 3.0 | 3.2 |

查看答案和解析>>
科目:初中物理 來源:2011-2012學年陜西省西安市交大陽光中學八年級(下)第一次月考物理試卷(解析版) 題型:選擇題
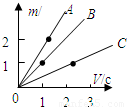
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com