日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

如果a,b為給定的實數，且1＜a＜b,1,a+1,2a+b,a+b+1這四個數據的平均數與中位數之差的絕對值是         .

已知M、N兩點關于y軸對稱，且點M在雙曲線y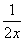＝上，點N在直線y＝x＋3上，設點M的坐標為(a，b)，則二次函數y＝－abx²＋(a＋b)x的最大值為________．

已知實數滿足        。

二次函數y=的圖象如圖，對稱軸為．若關于的一元二次方程（為實數）在的范圍內有解，則的取值范圍是(    )

A．    　　               B．

C．  　　　                D．

如圖，平面內4條直線l₁、l₂、 l₃、 l₄是一組平行線，相鄰2條平行線的距離都是1個單位長度，正方形ABCD的4個頂點A、B、C、D都在這些平行線上，則這個正方形的面積不可能是（    ）平方單位。

A. 1         B. 3          C. 5           D. 9

已知整數x,y 滿足，那么整數對（x,y）的個數是（   ）

A. 1           B. 3          C. 0           D. 2

如圖，已知直線與雙曲線交于A、B兩點，點B坐標為，C為雙曲線上一點，且在第一象限內，若面積為6，則點C坐標為（      ）

A.（4,2）       B.（2,3）        C.（3,4）     D.（2,4）

 如圖，是根據媒體提供的消息繪制的“寧波各大報刊發行量統計圖”，那么發行量的眾數是（    ）

A.寧波晚報     B.寧波日報和東南商報    C.33萬     D.22萬

．閱讀理解并填空：

（1）為了求代數式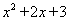的值，我們必須知道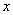的值．若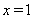，則這個代數式的值為_______；若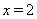，則這個代數式的值為_______，……，可見，這個代數式的值因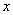的取值不同而_______（填“變化”或“不變”）．盡管如此，我們還是有辦法來考慮這個代數式的值的范圍．

（2）把一個多項式進行部分因式分解可以來解決代數式值的最大（或最小）值問題．例如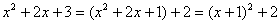：，因為是非負數，所以，這個代數式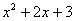的最小值是_______，這時相應的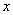的值是__________．

嘗試探究并解答：

（3）求代數式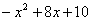的最大（或最小）值，并寫出相應的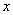的值．

（4）求代數式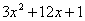的最大（或最小）值，并寫出相應的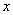的值．

（5）已知，且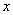的值在數1～4（包含1和4）之間變化，求這時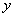的變化范圍．

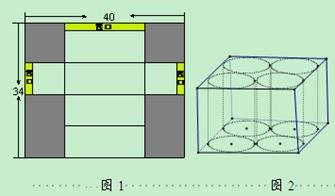
小葉爸爸開了一家茶葉專賣店．包裝設計專業畢業的小葉為他爸設計了一款用長方形厚紙片（厚度不計）做長方體茶葉包裝盒（如圖），陰影部分是裁剪掉的部分．沿圖中實線折疊做成的長方體紙盒的上下底面是正方形，有三處矩形形狀的“接口”用來折疊后粘貼或封蓋．

（1）若小葉用長40cm，寬34cm的矩形厚紙片，恰好能做成一個符合要求的包裝盒，盒高是盒底邊長的2.5倍，三處“接口”的寬度相等．則該茶葉盒的容積是多少？

（2）小葉爸爸的茶葉專賣店以每盒150元購進一批茶葉，按進價增加20%作為售價，第一個月由于包裝粗糙，只售出不到一半但超過三分之一的量；第二個月采用了小葉的包裝后，馬上售完了余下的茶葉，但成本增加了每盒5元，售價仍不變．已知在整個買賣過程中共盈利1500元，求這批茶葉共進了多少盒？