
科目: 來源: 題型:
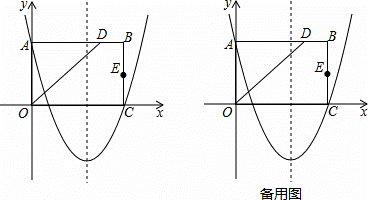
如圖,在平面直角坐標系中,矩形OABC的邊OA在y軸的正半軸上,OC在x軸的正半軸上,∠AOC的平分線交AB于點D,E為BC的中點,已知A(0,4)、C(5, 0),二次函數y=
0),二次函數y=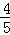 x2+bx+c的圖象拋物線經過A,C兩點.
x2+bx+c的圖象拋物線經過A,C兩點.
(1)求該二次函數的表達式;
(2)F、G分別為x軸,y軸上的動點,順次連接D、E、F、G構成四邊形DEFG,求四邊形DEFG周長的最小值;
(3)拋物線上是否在點P,使△ODP的面積為12?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
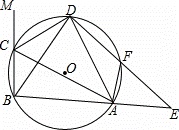
在△ABC的外接圓⊙O中,△ABC的外角平分線CD交⊙O于點D,F為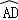 上﹣
上﹣
點,且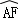 =
=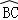 連接DF,并延長DF交BA的延長線于點E.
連接DF,并延長DF交BA的延長線于點E.
(1)判斷DB與DA的數量關系,并說明理由;
(2)求證:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半徑為5,DC=6,求DE的長.
查看答案和解析>>
科目: 來源: 題型:
閱讀與應用:
閱讀1:a、b為實數,且a>0,b>0,因為(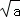 ﹣
﹣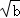 )2≥0,所以a﹣2
)2≥0,所以a﹣2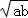 +b≥0從而a+b≥2
+b≥0從而a+b≥2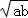 (
( 當a=b時取等號).
當a=b時取等號).
閱讀2:若函數y=x+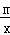 ;(m>0,x>0,m為常數),由閱讀1結論可知:x+
;(m>0,x>0,m為常數),由閱讀1結論可知:x+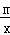 ≥2
≥2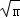 ,所以當x=
,所以當x=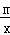 ,即x=
,即x=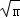 時,函數y=x+
時,函數y=x+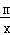 的最小值為2
的最小值為2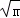 .
.
閱讀理解上述內容,解答下列問題:
問題1:已知一個矩形的面積為4,其中一邊長為x,則另一邊長為 ,周長為2(x+
,周長為2(x+ ),求當x= 時,周長的最小值為 ;
),求當x= 時,周長的最小值為 ;
問題2:已知函數y1=x+1(x>﹣1)與函數y2=x2+2x+10(x>﹣1),
當x= 時,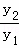 的最小值為 ;
的最小值為 ;
問題3:某民辦學校每天的支出總費用包含以下三個部分:一是教職工工資4900元;二是學生生活費成本每人10元;三是其他費用.其中,其他費用與學生人數的平方成正比,比例系數為0.01.當學校學生人數為多少時,該校每天生均投入最低?最低費用是多少元?(生均投入=支出總費用÷學生人數)
查看答案和解析>>
科目: 來源: 題型:
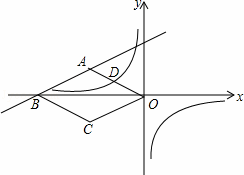
如圖,在平面直角坐標系中,四邊形ABCD是菱形,B、O在x軸負半軸上,AO=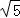 ,tan∠AOB=
,tan∠AOB=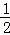 ,一次函數y=k1x+b的圖象過A、B兩點,反比例函數y=
,一次函數y=k1x+b的圖象過A、B兩點,反比例函數y= 的圖象過OA的中點D.
的圖象過OA的中點D.
(1)求一次函數和反比例函數的表達式;
(2)平移一次函數y=k1x+b的圖象,當一次函數y=k1x+b的圖象與反比例函數y=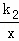 的圖象無交點時,求b的取值范圍.
的圖象無交點時,求b的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com