
【題目】如圖,在![]() 中,
中, ![]() ,
, ![]() 于點
于點![]() ,把線段
,把線段![]() 沿著
沿著![]() 的方向平移
的方向平移![]() 得到線段
得到線段![]() ,連接
,連接![]() .
.
問:(1)四邊形![]() 是_________形;
是_________形;
(2)若![]() 的周長比
的周長比![]() 的周長大6,求四邊形
的周長大6,求四邊形![]() 的面積.
的面積.
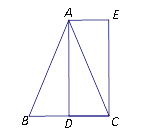
【答案】(1)矩;(2)60.
【解析】試題分析:(1)先由![]() 可得BD=CD, ∠ADC=90°,由平移可得BD∥AE,
可得BD=CD, ∠ADC=90°,由平移可得BD∥AE,
四邊形ADCE是平行四邊形,由∠ADC=90°得平行四邊形ADCE是矩形;(2)![]() ,
, ![]() ,由
,由![]() 的周長比
的周長比![]() 的周長大6及勾股定理得方程組
的周長大6及勾股定理得方程組![]() ,解得
,解得![]() 的值,即可得出矩形
的值,即可得出矩形![]() 的面積.
的面積.
試題解析:(1)
∵![]() 于點
于點![]() ,
,
∴BD=CD, ∠ADC=90°,
由平移可得BD∥AE,且BD=AE,
∴CD∥AE,且CD=AE,
∴四邊形ADCE是平行四邊形,
∵∠ADC=90°,
∴平行四邊形ADCE是矩形.
(2)∵四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() .
.
設![]() ,
, ![]()
∵![]() 的周長比
的周長比![]() 的周長大6,
的周長大6,
∴![]() ,即
,即![]() ①
①
在![]() 中,由勾股定理得:
中,由勾股定理得: ![]() ,即
,即![]() ②
②
由② -①的平方,得: ![]() ,
, ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在一棵樹CD的10m高處的B點有兩只猴子,它們都要到A處池塘邊喝水,其中一只猴子沿樹爬下走到離樹20m處的池塘A處,另一只猴子爬到樹頂D后直線躍入池塘的A處.如果兩只猴子所經過的路程相等,試問這棵樹多高? 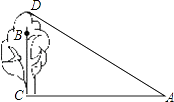
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年“五一”假期期間,某市接待旅游總人數達到了9 180 000人次,將9 180 000用科學記數法表示應為( )
A.918×104
B.9.18×105
C.9.18×106
D.9.18×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知am=3,an=4,化簡下列各式:(1)am+1=______; (2)a3+n=_______; (3)am+n+2=_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:(1)(-2)×(-2)2×(-2)3=_____________; (2)(-x)9·x5·(-x)5·(-x)3=___________;(3)an+4·a2n-1·a____________;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于點P(x,y),我們把點P′(﹣y+1,x+1)叫作點P的伴隨點.已知點A1的伴隨點為A2,點A2的伴隨點為A3,點A3的伴隨點為A4,這樣依次得到點A1,A2,A3,A4…,若點A1的坐標為(a,b),對于任意的正整數n,點An均在x軸上方,則a,b應滿足的條件為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若將一個自然數各位上的數字按照從高位數字到低位數字排成一列后,后一個人數減去前一個數的差是一個常數,則這個數叫做“幸福數”.如:四位數2468排成一列后為:2,4,6,8.因為8-6=6-4=4-2=2,且差為2的常數,故2468是一個差為2的四位“幸福數”.又如,9876,6666等也是“幸福數”.
若一個自然數從左到右各數位上的數字和另一個自然數從右到左各數位上的數字完全相同,則稱這兩個數為“三生三世數”.例如:3579與9753,8765與5678,...,都是“三生三世數”.
規定:把高位數字為x,差為2的三位“幸福數”與它的“三生三世數”的和與222的商記為F(x).例如當x=5時,三位“幸福數”為579,它的“三生三世數”為975,三位“幸福數”與它的“三生三世數”的和為:579+975=1554,1554÷222=7,所以F(x)=7.
(1)計算:F(1), F(4);
(2)已知F(x) =4,求x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com