
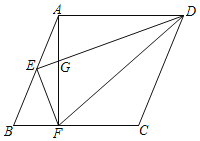
【題目】如圖,已知菱形ABCD,點(diǎn)E是AB的中點(diǎn),AF⊥BC于點(diǎn)F,連接EF,ED,DF,DE交AF于點(diǎn)G,且AE2=EGED.求證:DE⊥EF.

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
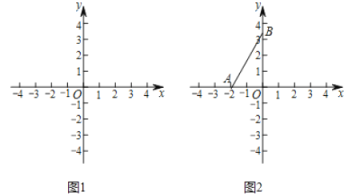
【題目】在平面直角坐標(biāo)系![]() 中,
中,![]() 的半徑為
的半徑為![]() ,點(diǎn)
,點(diǎn)![]() 與圓心
與圓心![]() 不重合,給出如下定義:若在
不重合,給出如下定義:若在![]() 上存在一點(diǎn)
上存在一點(diǎn)![]() ,使
,使![]() ,則稱點(diǎn)
,則稱點(diǎn)![]() 為
為![]() 的特征點(diǎn).
的特征點(diǎn).
(1)當(dāng)![]() 的半徑為1時(shí),如圖1.
的半徑為1時(shí),如圖1.
①在點(diǎn)![]() ,
,![]() ,
,![]() 中,
中,![]() 的特征點(diǎn)是__________.
的特征點(diǎn)是__________.
②點(diǎn)![]() 在直線
在直線![]() 上,若點(diǎn)
上,若點(diǎn)![]() 為
為![]() 的特征點(diǎn),求
的特征點(diǎn),求![]() 的取值范圍.
的取值范圍.
(2)如圖2,![]() 的圓心在
的圓心在![]() 軸上,半徑為2,點(diǎn)
軸上,半徑為2,點(diǎn)![]() ,
,![]() .若線段
.若線段![]() 上的所有點(diǎn)都是
上的所有點(diǎn)都是![]() 的特征點(diǎn),直接寫出圓心
的特征點(diǎn),直接寫出圓心![]() 的橫坐標(biāo)
的橫坐標(biāo)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】每年的![]() 月
月![]() 日為世界環(huán)保日,為了提倡低碳環(huán)保,某公司決定購買
日為世界環(huán)保日,為了提倡低碳環(huán)保,某公司決定購買![]() 臺節(jié)省能源的新設(shè)備,現(xiàn)有甲、乙兩種型號的設(shè)備可供選購.經(jīng)調(diào)查:購買
臺節(jié)省能源的新設(shè)備,現(xiàn)有甲、乙兩種型號的設(shè)備可供選購.經(jīng)調(diào)查:購買![]() 臺甲型設(shè)備比購買
臺甲型設(shè)備比購買![]() 臺乙型設(shè)備多花
臺乙型設(shè)備多花![]() 萬元,購買
萬元,購買![]() 臺甲型設(shè)備比購買
臺甲型設(shè)備比購買![]() 臺乙型設(shè)備少花
臺乙型設(shè)備少花![]() 萬元.
萬元.
(1)求甲、乙兩種型號設(shè)備每臺的價(jià)格;
(2)該公司經(jīng)決定購買甲型設(shè)備不少于![]() 臺,預(yù)算購買節(jié)省能源的新設(shè)備資金不超過
臺,預(yù)算購買節(jié)省能源的新設(shè)備資金不超過![]() 萬元,你認(rèn)為該公司有哪幾種購買方案;
萬元,你認(rèn)為該公司有哪幾種購買方案;
(3)在(2)的條件下,已知甲型設(shè)備每月的產(chǎn)量為![]() 噸,乙型設(shè)備每月的產(chǎn)量為
噸,乙型設(shè)備每月的產(chǎn)量為![]() 噸.若每月要求產(chǎn)量不低于
噸.若每月要求產(chǎn)量不低于![]() 噸,為了節(jié)約資金,請你為該公司設(shè)計(jì)一種最省錢的購買方案.
噸,為了節(jié)約資金,請你為該公司設(shè)計(jì)一種最省錢的購買方案.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下面所示各圖是在同一直角坐標(biāo)系內(nèi),二次函數(shù)y=![]() +(a+c)x+c與一次函數(shù)y=ax+c的大致圖象.正確的( )
+(a+c)x+c與一次函數(shù)y=ax+c的大致圖象.正確的( )
A. 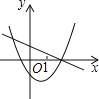 B.
B. 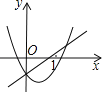 C.
C. 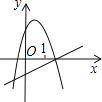 D.
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形紙片![]() ,
,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是
是![]() 上一動(dòng)點(diǎn),
上一動(dòng)點(diǎn),![]() 沿
沿![]() 折疊,點(diǎn)
折疊,點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處;延長
處;延長![]() 交
交![]() 于
于![]() 點(diǎn),連接
點(diǎn),連接![]() .
.
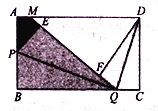
(1)求證:![]() ≌
≌![]() ;
;
(2)當(dāng)![]() 時(shí),將
時(shí),將![]() 沿
沿![]() 折疊,點(diǎn)
折疊,點(diǎn)![]() 落在線段
落在線段![]() 上點(diǎn)
上點(diǎn)![]() 處.
處.
①求證:![]() ∽
∽![]() ;
;
②如果![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,∠A=60°,點(diǎn)O為AB上一點(diǎn),且3AO=AB,以OA為半徑作半圓O,交AC于點(diǎn)D,AB于點(diǎn)E,DE與OC相交于F.
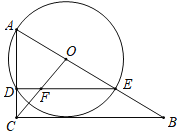
(1)求證:CB與⊙O相切;
(2)若AB=6,求DF的長度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】黃石市在創(chuàng)建國家級文明衛(wèi)生城市中,綠化檔次不斷提升.某校計(jì)劃購進(jìn)A,B兩種樹木共100棵進(jìn)行校園綠化升級,經(jīng)市場調(diào)查:購買A種樹木2棵,B種樹木5棵,共需600元;購買A種樹木3棵,B種樹木1棵,共需380元.
(1)求A種,B種樹木每棵各多少元?
(2)因布局需要,購買A種樹木的數(shù)量不少于B種樹木數(shù)量的3倍.學(xué)校與中標(biāo)公司簽訂的合同中規(guī)定:在市場價(jià)格不變的情況下(不考慮其他因素),實(shí)際付款總金額按市場價(jià)九折優(yōu)惠,請?jiān)O(shè)計(jì)一種購買樹木的方案,使實(shí)際所花費(fèi)用最省,并求出最省的費(fèi)用.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有甲、乙、丙三人組成的籃球訓(xùn)練小組,他們?nèi)酥g進(jìn)行互相傳球練習(xí),籃球從一個(gè)人手中隨機(jī)傳到另外一個(gè)人手中計(jì)作傳球一次,共連續(xù)傳球三次.
(1)若開始時(shí)籃球在甲手中,則經(jīng)過第一次傳球后,籃球落在丙的手中的概率是 ;
(2)若開始時(shí)籃球在甲手中,求經(jīng)過連續(xù)三次傳球后,籃球傳到乙的手中的概率.(請用畫樹狀圖或列表等方法求解)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,拋物線![]() 的對稱軸為
的對稱軸為![]() ,與
,與![]() 軸的交點(diǎn)
軸的交點(diǎn)![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
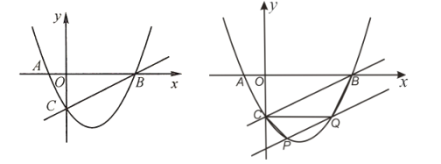
(1)求拋物線的解析式;
(2)點(diǎn)![]() 是直線
是直線![]() 下方拋物線上的一點(diǎn),過點(diǎn)
下方拋物線上的一點(diǎn),過點(diǎn)![]() 作
作![]() 的平行線交拋物線于點(diǎn)
的平行線交拋物線于點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 右側(cè)),連結(jié)
右側(cè)),連結(jié)![]() 、
、![]() ,當(dāng)
,當(dāng)![]() 的面積為
的面積為![]() 面積的一半時(shí),求
面積的一半時(shí),求![]() 點(diǎn)的坐標(biāo);
點(diǎn)的坐標(biāo);
(3)現(xiàn)將該拋物線沿射線![]() 的方向進(jìn)行平移,平移后的拋物線與直線
的方向進(jìn)行平移,平移后的拋物線與直線![]() 的交點(diǎn)為
的交點(diǎn)為![]() 、
、![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的下方),與
的下方),與![]() 軸的右側(cè)交點(diǎn)為
軸的右側(cè)交點(diǎn)為![]() ,當(dāng)
,當(dāng)![]() 與
與![]() 相似,求出點(diǎn)
相似,求出點(diǎn)![]() 的橫坐標(biāo).
的橫坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com