Question

（2011山東煙臺，26，14分）

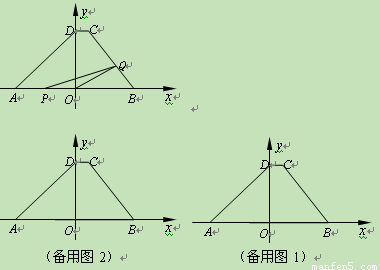
如圖，在直角坐標系中，梯形ABCD的底邊AB在x軸上，底邊CD的端點D在y軸上.直線CB的表達式為y=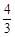－x+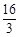，點A、D的坐標分別為（－4，0），（0，4）.動點P自A點出發，在AB上勻速運行.動點Q自點B出發，在折線BCD上勻速運行，速度均為每秒1個單位.當其中一個動點到達終點時，它們同時停止運動.設點P運動t（秒）時，△OPQ的面積為s（不能構成△OPQ的動點除外）.

（1）求出點B、C的坐標；

（2）求s隨t變化的函數關系式；

（3）當t為何值時s有最大值？并求出最大值.

 

Answer 1

【答案】

 

（1）把y＝4代入y＝－x＋，得x＝1.

 ∴C點的坐標為（1，4）.

 

當y＝0時，－x＋＝0，

∴x＝4.∴點B坐標為（4，0）.

（2）作CM⊥AB于M，則CM＝4，BM＝3.

∴BC＝＝＝5.

∴sin∠ABC＝＝.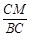

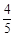①當0＜t＜4時，作QN⊥OB于N，

則QN＝BQ·sin∠ABC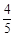＝t.

∴S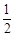＝OP·QN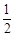＝（4－t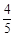）×t ＝－t²＋t（0＜t＜4）.

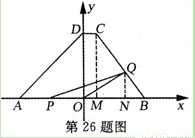
②當4＜t≤5時，（如備用圖1），

連接QO，QP，作QN⊥OB于N.

同理可得QN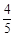＝t.

∴S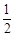＝OP·QN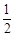＝×（t－4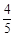）×t.

＝t²－t（4＜t≤5）.

③當5＜t≤6時，（如備用圖2），

連接QO，QP.

S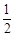＝×OP×OD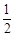＝（t－4）×4.

＝2t－8（5＜t≤6）.

（3）①在0＜t＜4時，

當t＝＝2時，

S_最大＝＝.

②在4＜t≤5時，對于拋物線S＝t²－t，當t＝－＝2時，

S_最小＝×2²－×2＝－.

∴拋物線S＝t²－t的頂點為（2，－）.

∴在4＜t≤5時，S隨t的增大而增大.

∴當t＝5時，S_最大＝×5²－×5＝2.

③在5＜t≤6時，

在S＝2t－8中，∵2＞0，∴S隨t的增大而增大.

∴當t＝6時，S_最大＝2×6－8＝4.

∴綜合三種情況，當t＝6時，S取得最大值，最大值是4.

【解析】略