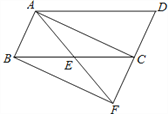
【題目】如圖，已知E是平行四邊形ABCD中BC邊的中點，連接AE并延長AE交DC的延長線于點F。
（1）求證：△ABE≌△FCE；
（2）連接AC、BF，若AE＝
BC，求證：四邊形ABFC為矩形；
（3）在（2）條件下，當△ABC再滿足一個什么條件時，四邊形ABFC為正方形。
【答案】（1）證明見解析；（2）證明見解析；（3）當AB＝AC時，矩形ABFC為正方形.
【解析】試題分析：（1）根據平行四邊形的性質可得到AB∥CD，從而可得到AB∥DF，根據平行線的性質可得到兩組角相等，已知點E是BC的中點，從而可根據AAS來判定△BAE≌△CFE；
（2）根據全等三角形的對應邊相等可證得AB=CF．再根據已知可得BC=AF，從而得證；
（3）矩形ABFC要想成為正方形，只只需要一組鄰邊相等即可，由此可添另條件AB=AC.
試題解析：（1）在 
ABCD中，AB∥CD ,AB＝CD，∴ ∠BAE＝∠EFC，
∵ E為BC的中點 ，∴ BE＝EC，
∵ ∠AEB＝∠FEC，∴ △ABE≌△FCE；
（2）由（1）知AB∥CD ， 即 AB∥CF，
∵△ABE≌△FCE ，∴ AB＝FC，
∴ 四邊形ABFC為平行四邊形 ，∴ AE＝EF＝
AF，
∵ AE＝BC ， ∴ BC＝AF ， ∴ABFC是矩形；
（3）當△ABC為等腰三角形時，即 AB＝AC時，矩形ABFC為正方形.
科目：初中數學 來源： 題型：
【題目】閱讀新知：移項且合并同類項之后，只含有偶次項的四次方程稱作雙二次方程．其一般形式為ax4＋bx2＋c＝0(a≠0)，一般通過換元法解之，具體解法是設 x2＝y，則原四次方程化為一元二次方程：ay2＋by＋c＝0，解出y之后代入x2＝y，從而求出x的值．
例如解：4x4－8x2＋3＝0
解：設x2＝y，則原方程可化為：4y2－8y＋3＝0
∵a＝4，b＝－8，c＝3
∴b2－4ac＝(－8)2－4×4×3＝16＞0
∴y＝
＝
∴y1＝
， y2＝
∴當y1＝時，x2＝． ∴x1＝
，x2＝－；
當y1＝時，x2＝． ∴x3＝
，x4＝－．
小試牛刀：請你解雙二次方程：x4－2x2－8＝0
歸納提高：
思考以上解題方法，試判斷雙二次方程的根的情況，下列說法正確的是____________(選出所有的正確答案)
①當b2－4ac≥0時，原方程一定有實數根；
②當b2－4ac＜0時，原方程一定沒有實數根；
③當b2－4ac≥0，并且換元之后的一元二次方程有兩個正實數根時，原方程有4個實數根，換元之后的一元二次方程有一個正實數根一個負實數根時，原方程有2個實數根；
④原方程無實數根時，一定有b2－4ac＜0．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2015年在中國等發展中國家的帶動下，全球可持續投資再創歷史新高，達1550億美元，這個數據用科學記數法可表示為（ ）美元．
A.1.55×1010
B.1.55×1011
C.1.55×1012
D.1.55×1013
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有人說，將一張紙對折，再對折，重復下去，第43次后紙的厚度便超過地球到月球的距離，已知一張紙厚0.006cm，地球到月球的距離約為3.85×108m，用計算器算一下這種說法是否可信．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用直尺和圓規作一個角等于已知角的示意圖如右，則說明∠A′O′B′=∠AOB的依據是（ ）
A. SSS B. SAS C. ASA D. AAS
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知△ABC的三個頂點的坐標分別為A（－3，5），B（－2，1），C（－1，3）．
（1）畫出△ABC關于x軸的對稱圖形△A1B1C1；
（2）畫出△A1B1C1沿x軸向右平移4個單位長度后得到的△A2B2C2；
（3）如果AC上有一點M（a，b）經過上述兩次變換，那么對應A2C2上的點M2的坐標是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小紅駕車從甲地到乙地，她出發第xh時距離乙地ykm，已知小紅駕車中途休息了1小時，圖中的折線表示她在整個駕車過程中y與x之間的函數關系．
（1）B點的坐標為（ ， ）；
（2）求線段AB所表示的y與x之間的函數表達式；
（3）小紅休息結束后，以60km/h的速度行駛，則點D表示的實際意義是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某特產專賣店銷售核桃，其進價為每千克40元，按每千克60元出售，平均每天可售出100千克，后來經過市場調查發現，單價每降低2元，則平均每天的銷售可增加20千克，若該專賣店銷售這種核桃要想平均每天獲利2240元，請回答：
（1）每千克核桃應降價多少元？
（2）在平均每天獲利不變的情況下，為盡可能讓利于顧客，贏得市場，該店應按原售價的幾折出售？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠ABC=90°，D是直線AB上的點，AD=BC，如圖，過點A作AF⊥AB，并截取AF=BD，連接DC、DF、CF．
（1）求證：△FAD≌△DBC；
（2）判斷△CDF的形狀并證明．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com