【題目】某廠準備購買
、
、
三種配件共
件，要求購買時
配件的件數是
配件數的
倍， 
配件不超過
件，且每種配件都必須買，三種配件的價格如下： 
、
、
三種配件的單價分別為
元、
元、
元．
（
）求購買
配件的件數范圍．
（
）三種配件應各買多少件，才能使買配件的總費用最少？總費用最少多少元？
【答案】（1）
；（2）
配件買
件， 
配件買
件， 
配件買
件，所需總費用最少
元．
【解析】試題分析：（1）設買A種配件x件，B種配件（1000-5x）件，C種配件4x件，根據B配件不超過400件列出不等式組，解不等式組即可得x的取值范圍；（2）設總費用為y元，根據題意列出y與x的函數關系式，根據x的取值范圍和一次函數的性質可得即可解決問題.
試題解析：
（1）設買A種配件x件，B種配件（1000-5x）件，C種配件4x件，因為B配件不超過400件，所以0<1000-5x≤400，即可得120≤x<200．
（2）設總費用為y元，根據題意得：y=30x+(1000-5x)×50+80×40x=100x+50000(120≤x<200)．
當x=120時，y最小，y=100×120+50000=62000（元），1000-5x=400，4x=480．
答： A配件買120件，B配件買400件，C配件買480件，所需總費用最少為62000元．
科目：初中數學 來源： 題型：
【題目】如圖，在¨ABCD中，過點D作DE⊥AB與點E，點F在邊CD上，DF=BE,連接AF,BF
（1）求證：四邊形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求證：AF平分∠DAB.
查看答案和解析>>
科目：初中數學 來源： 題型：
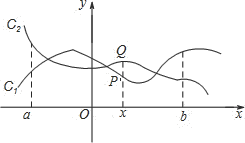
【題目】如圖，點
與
分別是兩個函數圖象
與
上的任一點．當
時，有
成立，則稱這兩個函數在
上是“相鄰函數”，否則稱它們在
上是“非相鄰函數”．例如，點
與
分別是兩個函數
與
圖象上的任一點，當
時， 
，通過構造函數
并研究它在
上的性質，得到該函數值得范圍是
，所以
成立，因此這兩個函數在
上是“相鄰函數”．
（
）判斷函數
與
在
上是否為“相鄰函數”，并說明理由．
（
）若函數
與
在
上是“相鄰函數”，求
的取值范圍．
（
）若函數
與
在
上是“相鄰函數”，直接寫出
的最大值與最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用數學的方式理解“當窗理云鬢，對鏡貼花黃”和“坐地日行八萬里”（只考慮地球的自轉），其中蘊含的圖形運動是（ ）
A.平移和旋轉
B.對稱和旋轉
C.對稱和平移
D.旋轉和平移
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把直角三角形ABC的斜邊AB放在定直線l上，按順時針方向在l上轉動兩次，使它轉到△A″B″C″的位置．設BC=2，AC=2
，則頂點A運動到點A″的位置時，點A經過的路線與直線l所圍成的面積是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com