
【題目】在一次數學興趣小組活動中,小明利用同弧所對的圓周角及圓心角的性質探索了一些問題,下面請你和小明一起進入探索之旅.
問題情境:
(![]() )如圖,
)如圖, ![]() 中,
中, ![]() ,
, ![]() ,則
,則![]() 的外接圓的半徑為__________.
的外接圓的半徑為__________.

操作實踐:
(![]() )如圖,在矩形
)如圖,在矩形![]() 中,請利用以上操作所獲得的經驗,在矩形
中,請利用以上操作所獲得的經驗,在矩形![]() 內部用直尺與圓規作出一點
內部用直尺與圓規作出一點![]() .點
.點![]() 滿足:
滿足: ![]() ,且
,且![]() .
.
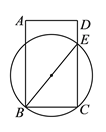
(要求:用直尺與圓規作出點![]() ,保留作圖痕跡.)
,保留作圖痕跡.)
遷移應用:
(![]() )如圖,在平面直角坐標系的第一象限內有一點
)如圖,在平面直角坐標系的第一象限內有一點![]() ,坐標為
,坐標為![]() .過點
.過點![]() 作
作![]() 軸,
軸, ![]() 軸,垂足分別為
軸,垂足分別為![]() 、
、![]() ,若點
,若點![]() 在線段
在線段![]() 上滑動(點
上滑動(點![]() 可以與點
可以與點![]() 、
、![]() 重合),發現使得
重合),發現使得![]() 的位置有兩個,則
的位置有兩個,則![]() 的取值范圍為__________.
的取值范圍為__________.

【答案】(1)2;(2)作圖見解析;(3)![]()
【解析】試題分析:(1)連接OB、OC,只要證明△OBC是等邊三角形即可.
(2)如圖2中,作BC的垂直平分線,交BE于點O,以O為圓心,OB為半徑作圓,交垂直平分線于點P,則點P為所求.
(3)如圖3中,在x軸上方作△OKC,使得△OKC是以OC為斜邊的等腰直角三角形,作KE⊥AB于E.當EK=KC=![]() 時,以K為圓心,KC為半徑的圓與AB相切,此時m=BC=1+
時,以K為圓心,KC為半徑的圓與AB相切,此時m=BC=1+![]() ,在AB上只有一個點P滿足∠OPC=
,在AB上只有一個點P滿足∠OPC=![]() ∠OKC=45°,當BK=
∠OKC=45°,當BK=![]() 時,在AB上恰好有兩個點P滿足∠OPC=
時,在AB上恰好有兩個點P滿足∠OPC=![]() ∠OKC=45°,此時m=BC=2,由此不難得出結論.
∠OKC=45°,此時m=BC=2,由此不難得出結論.
試題解析:解:(1)如圖1中,連接OB、OC.

∵∠BOC=2∠A,∠A=30°,∴∠BOC=60°,∵OB=OC,∴△OBC是等邊三角形,∴OB=OC=BC=2,故答案為:2.
(2)如圖2中,作BC的垂直平分線,交BE于點O;
以O為圓心,OB為半徑作圓,交垂直平分線于點P,則點P為所求.
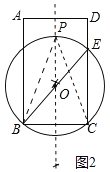
(3)如圖3中,在x軸上方作△OKC,使得△OKC是以OC為斜邊的等腰直角三角形,作KE⊥AB于E.

∵OC=2,∴OK=KC=![]() ,當EK=KC=
,當EK=KC=![]() 時,以K為圓心,KC為半徑的圓與AB相切,此時m=BC=1+
時,以K為圓心,KC為半徑的圓與AB相切,此時m=BC=1+![]() ,在AB上只有一個點P滿足∠OPC=
,在AB上只有一個點P滿足∠OPC=![]() ∠OKC=45°,當BK=
∠OKC=45°,當BK=![]() 時,在AB上恰好有兩個點P滿足∠OPC=
時,在AB上恰好有兩個點P滿足∠OPC=![]() ∠OKC=45°,此時m=BC=2.
∠OKC=45°,此時m=BC=2.
綜上所述,滿足條件的m的值的范圍為2≤m<1+![]() .
.
故答案為:2≤m<1+![]() .
.


科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=13 cm,AC=20 cm,BC邊上的高為12 cm,則△ABC的面積是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC邊在直線a上,將△ABC繞點A順時針旋轉到位置①可得到點P1,此時AP1=![]() ;將位置①的三角形繞點P1順時針旋轉到位置②,可得到點P2,此時AP2=1+
;將位置①的三角形繞點P1順時針旋轉到位置②,可得到點P2,此時AP2=1+![]() ;將位置②的三角形繞點P2順時針旋轉到位置③,可得到點P3時,AP3=2+
;將位置②的三角形繞點P2順時針旋轉到位置③,可得到點P3時,AP3=2+![]() …按此規律繼續旋轉,直至得到點P2018為止,則AP2018為( )
…按此規律繼續旋轉,直至得到點P2018為止,則AP2018為( )
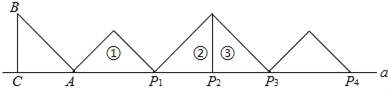
A. 1345+376![]() B. 2017+
B. 2017+![]() C. 2018+
C. 2018+![]() D. 1345+673
D. 1345+673![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小洋同學在筆記本上完成課堂練習的解題過程:
老師讓同桌互相核對,同桌小寧和小洋的答案不一樣,在仔細對比了自己和小洋書寫的過程后,小寧說:“你在第一步出現了兩個錯誤,導致最后錯了.”小洋自己檢查后發現,小寧說的是正確的.
解答下列問題:
(1)請你用標記符號“○”在以上小洋解答過程的第一步中錯誤之處;
(2)請重新寫出完成此題的解答過程.
(2x+1)(2x﹣1)﹣(x﹣3)2
小洋的解答:
(2x+1)(2x﹣1)﹣(x﹣3)2
=(2x)2﹣1﹣(x2﹣3x+9) 第一步
=2x2﹣1﹣x2+3x﹣9 第二步
=x2+3x﹣10. 第三步
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在 Rt△ABC 中,∠ACB=90°,O為AB邊上的一點,且![]() ,點D為AC邊上的動點(不與點A,C 重合),將線段OD繞點O順時針旋轉90°交BC于點E.
,點D為AC邊上的動點(不與點A,C 重合),將線段OD繞點O順時針旋轉90°交BC于點E.
(1)如圖1,若O為AB邊中點,D為AC邊中點,求![]() 的值;
的值;
(2)如圖2,若O為AB邊中點,D不是AC邊的中點,求![]() 的值。
的值。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形![]() 中,對角線
中,對角線![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 是
是![]() 上任意一點,連接
上任意一點,連接![]() ,過點
,過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,
,![]() 與
與![]() 交于點
交于點![]() .
.
(1)求證:![]() ;
;
(2)如圖2,若點![]() 在
在![]() 的延長線上,
的延長線上,![]() 于點
于點![]() ,
,![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,其他條件不變,判斷線段
,其他條件不變,判斷線段![]() 與
與![]() 的數量關系: .
的數量關系: .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC的邊OA,OC在坐標軸上,A(0,2),C(4,0).點P從點A出發,以每秒1個單位長度的速度沿射線AO方向運動,同時點Q從點C出發,以每秒2個單位的速度沿射線CO方向運動.設點P運動時間為t秒,(t>0)


(1)當t=1時,求△BPQ的周長;
(2)當t為何值時,△BPQ是等腰三角形;
(3)點C關于BQ的對稱點為C’,當C’恰好落在直線AQ上時,△BPQ的面積為__________.(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD平分∠BAC,按如下步驟作圖:
第一步,分別以點A、D為圓心,以大于![]() AD的長為半徑在AD兩側作弧,交于兩點M、N;第二步,連接MN分別交AB、AC于點E、F;第三步,連接DE、DF.
AD的長為半徑在AD兩側作弧,交于兩點M、N;第二步,連接MN分別交AB、AC于點E、F;第三步,連接DE、DF.
(1)求證:四邊形AEDF是菱形;
(2)若BD=6,AF=4,CD=3,求BE的長。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com