
【題目】如圖,在四邊形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,點M,N分別在AB,AD邊上,若AM:MB=AN:ND=1:2,則sin∠MCN=( ) 
A.![]()
B.![]()
C.![]()
D.![]() ﹣2
﹣2
【答案】B
【解析】解:∵AB=AD=6,AM:MB=AN:ND=1:2, ∴AM=AN=2,BM=DN=4,
連接MN,連接AC,
∵AB⊥BC,AD⊥CD,∠BAD=60°
在Rt△ABC與Rt△ADC中,![]() ,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAC=∠DAC= ![]() ∠BAD=30°,MC=NC,
∠BAD=30°,MC=NC,
∴BC= ![]() AC,
AC,
∴AC2=BC2+AB2 , 即(2BC)2=BC2+AB2 ,
3BC2=AB2 ,
∴BC=2 ![]() ,
,
在Rt△BMC中,CM= ![]() =2
=2 ![]() ,
,
∵AN=AM,∠MAN=60°,
∴△MAN是等邊三角形,
∴MN=AM=AN=2,
過M點作ME⊥CN于E,設NE=x,則CE=2 ![]() ﹣x,
﹣x,
∴MN2﹣NE2=MC2﹣EC2 , 即4﹣x2=(2 ![]() )2﹣(2
)2﹣(2 ![]() ﹣x)2 ,
﹣x)2 ,
解得:x= ![]() ,
,
∴EC=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
由勾股定理得:ME= ![]() =
= ![]() =
= ![]() ,
,
∴sin∠MCN= ![]() =
= ![]() =
= ![]() ,
,
故選B.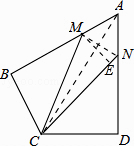
【考點精析】掌握相似三角形的判定與性質和解直角三角形是解答本題的根本,需要知道相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方;解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法).


科目:初中數學 來源: 題型:
【題目】已知:O是直線AB上的一點,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如圖1.若![]() .求
.求![]() 的度數;
的度數;
(2)在圖1中,![]() ,直接寫出
,直接寫出![]() 的度數(用含a的代數式表示);
的度數(用含a的代數式表示);
(3)將圖1中的![]() 繞頂點O順時針旋轉至圖2的位置,探究
繞頂點O順時針旋轉至圖2的位置,探究![]() 和
和![]() 的度數之間的關系.寫出你的結論,并說明理由.
的度數之間的關系.寫出你的結論,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分線BD交AC于點D,則AD的長是 , cosA的值是 . (結果保留根號) 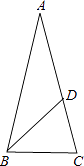
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為加快城市群的建設與發展,在A,B兩城市間新建一條城際鐵路,建成后,鐵路運行里程由現在的120km縮短至114km,城際鐵路的設計平均時速要比現行的平均時速快110km,運行時間僅是現行時間的![]() ,求建成后的城際鐵路在A,B兩地的運行時間.
,求建成后的城際鐵路在A,B兩地的運行時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設A=![]() .
.
(1)化簡A;
(2)當a=3時,記此時A的值為f(3);當a=4時,記此時A的值為f(4)……解關于x的不等式:![]() -
-![]() ≤f(3)+f(4)+…+f(11),并將它的解集在數軸上表示出來.
≤f(3)+f(4)+…+f(11),并將它的解集在數軸上表示出來.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設a1 , a2 , …,a2017是從1,0,﹣1這三個數中取值的一列數,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,則a1 , a2 , …,a2017中為0的個數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數量充足,某同學去該店購買飲料,每種飲料被選中的可能性相同.
(1)若他去買一瓶飲料,則他買到奶汁的概率是;
(2)若他兩次去買飲料,每次買一瓶,且兩次所買飲料品種不同,請用樹狀圖或列表法求出他恰好買到雪碧和奶油的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,AD是△ABC的角平分線,點O為AB的中點,連接DO并延長到點E,使OE=OD,連接AE,BE.
(1)求證:四邊形AEBD是矩形;
(2)當△ABC滿足什么條件時,矩形AEBD是正方形?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名射擊運動員中進行射擊比賽,兩人在相同條件下各射擊10次,射擊的成績如圖所示.

根據圖中信息,回答下列問題:
(1)甲的平均數是___________,乙的中位數是______________;
(2)分別計算甲、乙成績的方差,并從計算結果來分析,你認為哪位運動員的射擊成績更穩定?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com