【題目】若x+ 
=3,求 
的值.
【答案】解:∵x+ 
=3,
∴x2+ 
+2=9,即x2+ =7.∴ 
= 
= 
= 
【解析】方法一：將x+ =3兩邊同時平方，求出
的值，題中隱含x≠0.因此再將的分子和分母同時除以x2 ， 得到
，再整體代入計算即可；
方法二：求的倒數，即
，再代入值，然后取倒數即可得出原代數式的值。
【考點精析】解答此題的關鍵在于理解倒數的相關知識，掌握互為倒數：乘積為1的兩個數互為倒數；注意：0沒有倒數；若 a≠0，那么
的倒數是
；若ab=1? a、b互為倒數；若ab=-1? a、b互為負倒數，以及對代數式求值的理解，了解求代數式的值，一般是先將代數式化簡，然后再將字母的取值代入；求代數式的值，有時求不出其字母的值，需要利用技巧，“整體”代入．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
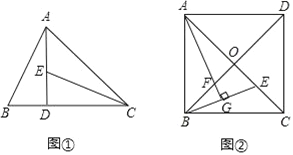
【題目】【閱讀發現】如圖①，在△ABC中，∠ACB=45°，AD⊥BC于點D，E為AD上一點，且DE=BD，可知AB=CE．
【類比探究】如圖②，在正方形ABCD中，對角線AC與BD交于點O，E是OC上任意一點，AG⊥BE于點G，交BD于點F．判斷AF與BE的數量關系，并加以證明．
【推廣應用】在圖②中，若AB=4，BF=
，則△AGE的面積為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】把拋物線y=2x2向上平移5個單位，所得拋物線的解析式為（ ）
A.y=2x2+5
B.y=2x2﹣5
C.y=2（x+5）2
D.y=2（x﹣5）2
查看答案和解析>>
科目：初中數學 來源： 題型：
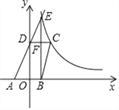
【題目】如圖，已知四邊形ABCD頂點A、B在x軸上，點D在y軸上，函數y=
（x＞0）的圖象經過點C（2，3），直線AD交雙曲線于點E，并且EB⊥x軸，CD⊥y軸，EB與CD交于點F．
（1）若EB=
OD，求點E的坐標；
（2）若四邊形ABCD為平行四邊形，求過A、D兩點的函數關系式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校準備購置甲乙兩種羽毛球拍若干，已知甲種球拍的單價比乙種球拍的單價多40元，且購買4副甲種球拍與購買6副乙種球拍的費用相同．
（1）兩種球拍的單價各是多少元？
（2）若學校準備購買100副甲乙兩種羽毛球拍，且購買甲種球拍的費用不少于乙種球拍費用的3倍，問購買多少副甲種球拍總費用最低？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我國最新研制的巨型計算機“曙光3000超級服務器”，它的運算峰值可以達到每秒403200000000次，403200000000用科學記數法來表示為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：△ABC是等邊三角形．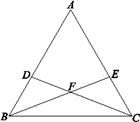
（1）如圖，點D在AB邊上，點E在AC邊上，BD＝CE，BE與CD交于點F． 試判斷BF與CF的數量關系，并加以證明；
（2）點D是AB邊上的一個動點，點E是AC邊上的一個動點，且BD＝CE，BE與CD交于點F．若△BFD是等腰三角形，求∠FBD的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
