
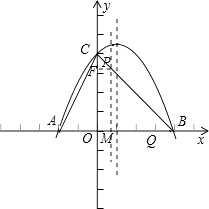
【題目】如圖,拋物線y=ax2+bx+4與x軸交于A(﹣2,0)、B(4、0)兩點,與y軸交于C點.
(1)求拋物線的解析式;
(2)T是拋物線對稱軸上的一點,且△ATC是以AC為底的等腰三角形,求點T的坐標;
(3)M、Q兩點分別從A、B點以每秒1個單位長度的速度沿x軸同時出發相向而行,當點M到原點時,點Q立刻掉頭并以每秒 ![]() 個單位長度的速度向點B方向移動,當點M到達拋物線的對稱軸時,兩點停止運動,過點M的直線l⊥x軸交AC或BC于點P.求點M的運動時間t與△APQ面積S的函數關系式,并求出S的最大值.
個單位長度的速度向點B方向移動,當點M到達拋物線的對稱軸時,兩點停止運動,過點M的直線l⊥x軸交AC或BC于點P.求點M的運動時間t與△APQ面積S的函數關系式,并求出S的最大值.
【答案】
(1)解:把A(﹣2,0),B(4,0)代入y=ax2+bx+4得:
![]() ,
,
解得:a=﹣ ![]() ,b=1,
,b=1,
∴拋物線的解析式是:y=﹣ ![]() x2+x+4,
x2+x+4,
答:拋物線的解析式是y=﹣ ![]() x2+x+4
x2+x+4
(2)解:由y=﹣ ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,得拋物線的對稱軸為直線x=1,
,得拋物線的對稱軸為直線x=1,
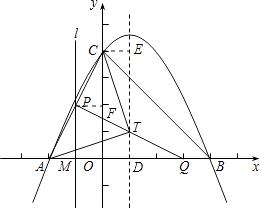
直線x=1交x軸于點D,設直線x=1上一點T(1,h),
連接TC、TA,作CE⊥直線x=1,垂足是E,
由C(0,4)得點E(1,4),
在Rt△ADT和Rt△TEC中,由TA=TC得32+h2=12+(4﹣h)2,
∴h=1,
∴T的坐標是(1,1),
答:點T的坐標是(1,1)
(3)解:(I)當0<t≤2時,△AMP∽△AOC,
∴ ![]() =
= ![]() ,PM=2t,
,PM=2t,
AQ=6﹣t,
∴S= ![]() PMAQ=
PMAQ= ![]() ×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,
當t=2時S的最大值為8;
(II)當2<t≤3時,
作PM⊥x軸于M,作PF⊥y軸于點F,
則△COB∽△CFP,
又∵CO=OB,
∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AQ=4+ ![]() (t﹣2)=
(t﹣2)= ![]() t+1,
t+1,
∴S= ![]() PMAQ=
PMAQ= ![]() (6﹣t)(
(6﹣t)( ![]() t+1)=﹣
t+1)=﹣ ![]() t2+4t+3=﹣
t2+4t+3=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
當t= ![]() 時,S最大值為
時,S最大值為 ![]() ,
,
綜合(I)(II)S的最大值為 ![]() ,
,
答:點M的運動時間t與△APQ面積S的函數關系式是S=﹣t2+6t(0<t≤2),S=﹣ ![]() t2+4t+3(2<t≤3),S的最大值是
t2+4t+3(2<t≤3),S的最大值是 ![]() .
.
【解析】(1)把A、B的坐標代入拋物線的解析式得到方程組,求出方程組的解即可;(2)設直線x=1上一點T(1,h),連接TC、TA,作CE⊥直線x=1,垂足是E,根據TA=TC由勾股定理求出即可;(3)(I)當0<t≤2時,△AMP∽△AOC,推出比例式,求出PM,AQ,根據三角形的面積公式求出即可;(II)當2<t≤3時,作PM⊥x軸于M,PF⊥y軸于點F,表示出三角形APQ的面積,利用配方法求出最值即可.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB⊥BC,DC⊥BC,垂足分別為B、C,設AB=4,DC=1,BC=4.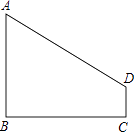
(1)求線段AD的長.
(2)在線段BC上是否存在點P,使△APD是等腰三角形?若存在,求出線段BP的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察如圖所示的長方體.

(1)用符號表示下列兩棱的位置關系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′與BC所在的直線是兩條不相交的直線,它們_____平行線.(填“是”或“不是”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校準備組織七年級學生參加夏令營,已知:用3輛小客車和1輛大客車每次可運送學生105人;用一輛小客車和2輛大客車每次可運送學生110人,現有學生400人,計劃租用小客車a輛,大客車b輛,一次送完,且恰好每輛車都坐滿.
(1)1輛小客車和1輛大客車都坐滿后一次可送多少名學生?
(2)請你幫學校設計出所有的租車方案;
(3)若小客車每輛需租金200元,大客車每輛需租金380元,請選出最省錢的方案,并求出最省租金.
查看答案和解析>>
科目:初中數學 來源: 題型:
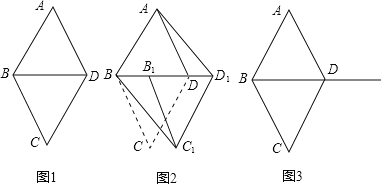
【題目】如圖1,![]() 和
和![]() 都是邊長為1的等邊三角形.
都是邊長為1的等邊三角形.
![]() 四邊形ABCD是菱形嗎?為什么?
四邊形ABCD是菱形嗎?為什么?
![]() 如圖2,將
如圖2,將![]() 沿射線BD方向平移到
沿射線BD方向平移到![]() 的位置,則四邊形
的位置,則四邊形![]() 是平行四邊形嗎?為什么?
是平行四邊形嗎?為什么?
![]() 在
在![]() 移動過程中,四邊形
移動過程中,四邊形![]() 有可能是矩形嗎?如果是,請求出點B移動的距離
有可能是矩形嗎?如果是,請求出點B移動的距離![]() 寫出過程
寫出過程![]() ;如果不是,請說明理由
;如果不是,請說明理由![]() 圖3供操作時使用
圖3供操作時使用![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
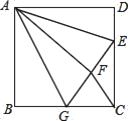
【題目】如圖,正方形ABCD中,AB=12,點E在邊CD上,且CD=3DE,將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG、CF,下列結論: ①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=28.8. 其中正確結論的個數是( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為建設資源節約型、環境友好型社會,克服因干旱而造成的電力緊張困難,切實做好節能減排工作.某地決定對居民家庭用電實行“階梯電價”,電力公司規定:居民家庭每月用電量在80千瓦時以下(含80千瓦時,1千瓦時俗稱1度)時,實行“基本電價”;當居民家庭月用電量超過80千瓦時時,超過部分實行“提高電價”.
(1)小張家今年2月份用電100千瓦時,上繳電費68元;5月份用電120千瓦時,上繳電費88元.求“基本電價”和“提高電價”分別為多少元/千瓦時;
(2)若6月份小張家預計用電130千瓦時,請預算小張家6月份應上繳的電費.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com