
關于![]() 的一元二次方程
的一元二次方程![]() 的一個根是2.
的一個根是2.
1.求![]() 的值和方程的另一個根
的值和方程的另一個根![]()
2.若直線AB經過點A(2,0),B(0,![]() ),求直線AB的解析式;
),求直線AB的解析式;
3.在平面直角坐標系中畫出直線AB的圖象,P是![]() 軸上一動點,是否存在點P,
軸上一動點,是否存在點P,
使△ABP是直角三角形,若存在,求出點P坐標,若不存在,說明理由.

1.∵2是一元二次方程![]() 的一個根,
的一個根,
∴![]() ,
,
∴![]() .-----------------------------------------------------------------------------------------2分
.-----------------------------------------------------------------------------------------2分
∴一元二次方程為![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴一元二次方程為![]() 的另一個根
的另一個根![]() =4.--------------------------------4分
=4.--------------------------------4分
2.設直線AB的解析式為![]()
∵直線AB經過點A(2,0),B(0,4)
∴![]()
解得![]() ,
,![]() .-------------------------------------------------------------------------------6分
.-------------------------------------------------------------------------------6分
直線AB的解析式:![]() .-------------------------------------------------------------8分
.-------------------------------------------------------------8分
3.畫圖正確----------------------------------------------------------------------------------------9分
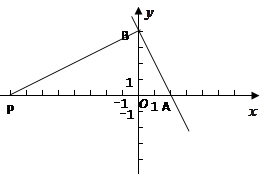
第一種:AB是斜邊,∠APB=90°
∵∠AOB=90°,
∴當點P與原點O重合時,∠APB=90°,
∴當點P的坐標為(0,0),△ABP是直角三角形.-----------------------------------------11分
第二種:設AB是直角邊,點B為直角頂點,即∠ABP=90°
∵線段AB在第一象限,
∴這時點P在![]() 軸負半軸.
軸負半軸.
設P的坐標為(![]() ,0)
,0)
∵A(2,0), B(0,4)
∴OA=2,OB=4,OP=![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
解得![]()
∴當點P的坐標為(―8,0),△ABP是直角三角形.-------------------------------------13分
第三種:設AB是直角邊,點A為直角頂點,即∠BAP=90°
∵點A在![]() 軸上,點P是
軸上,點P是![]() 軸上的動點,
軸上的動點,
∴∠BAP>90°
∴∠BAP=90°的情況不存在.-------------------------------------------------------------------14分
∴當點P的坐標為(―8,0)或(0,0)時,△ABP是直角三角形.
解析:略


科目:初中數學 來源:2011年河南省周口市九年級上學期聯考數學卷 題型:解答題
(本題滿分9分)定理:若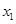 、
、 是關于
是關于 的一元二次方程
的一元二次方程 的兩實根,則有
的兩實根,則有 ,
, .請用這一定理解決問題:已知
.請用這一定理解決問題:已知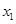 、
、 是關于
是關于 的一元二次方程
的一元二次方程 的兩實根,且
的兩實根,且 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com