
【題目】已知函數![]() 的圖象與
的圖象與![]() 軸有兩個公共點.
軸有兩個公共點.
(1)求![]() 的取值范圍,寫出當
的取值范圍,寫出當![]() 取范圍內最大整數時函數的解析式;
取范圍內最大整數時函數的解析式;
(2)題(1)中求得的函數記為C1
①當![]() 時,
時,![]() 的取值范圍是
的取值范圍是![]() ,求
,求![]() 的值;
的值;
②函數C2:![]() 的圖象由函數C1的圖象平移得到,其頂點P落在以原
的圖象由函數C1的圖象平移得到,其頂點P落在以原
點為圓心,半徑為![]() 的圓內或圓上.設函數C1的圖象頂點為M,求點P與點M距
的圓內或圓上.設函數C1的圖象頂點為M,求點P與點M距
離最大時函數C2的解析式.
【答案】(1)![]() 且
且![]() 當
當![]() 時,函數解析式為:
時,函數解析式為:![]() ;(2)①
;(2)①![]() ;②PM最大時的函數解析式為
;②PM最大時的函數解析式為![]() .
.
【解析】
試題分析: (1)函數![]() 的圖象與
的圖象與![]() 軸有兩個公共點.可知,根的判別式△>0,且m≠0,求得m的范圍
軸有兩個公共點.可知,根的判別式△>0,且m≠0,求得m的范圍![]() 且
且![]() 在此范圍內m取得最大整數2,解析式可寫出;(2)①根據函數增減性可以發現當x=n時,y=-3n,代入解析式求出
在此范圍內m取得最大整數2,解析式可寫出;(2)①根據函數增減性可以發現當x=n時,y=-3n,代入解析式求出![]() ;②求出C1的頂點M坐標為
;②求出C1的頂點M坐標為![]()
由圖像可知當PM經過圓心O時距離最大,求出直線PM的解析式為![]() 設出P點坐標,根據勾股定理就能求得P點坐標(2,1),C2解析式為
設出P點坐標,根據勾股定理就能求得P點坐標(2,1),C2解析式為![]() .
.
試題解析:(1)由題意可得: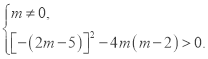 解得:
解得:![]() 且
且![]()
當![]() 時,函數解析式為:
時,函數解析式為:![]() .
.
(2)①函數![]() 圖象開口向上,對稱軸為
圖象開口向上,對稱軸為![]()
∴當![]() 時,
時,![]() 隨
隨![]() 的增大而減小.
的增大而減小.
∵當![]() 時,
時,![]() 的取值范圍是
的取值范圍是![]() ,
,
∴ ![]() .
.
∴ ![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
②∵![]()
∴圖象頂點![]() 的坐標為
的坐標為![]() ,
,
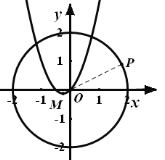
由圖形可知當![]() 為射線
為射線![]() 與圓的交點時,距離最大.
與圓的交點時,距離最大.
∵點P在直線OM上,由![]() 可求得直線解析式為:
可求得直線解析式為:![]() ,
,
設P(a,b),則有a=2b,
根據勾股定理可得![]()
求得![]() .
.
∴PM最大時的函數解析式為![]() .
.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】某商場服裝部為了解服裝的銷售情況,統計了每位營業員在某月的銷售額(單位:萬元),并根據統計的這組數據,繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題.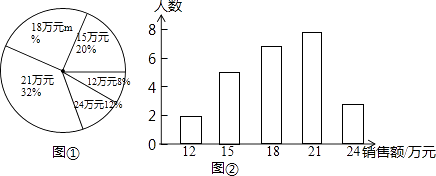
(1)該商場服裝部營業員的人數為 , 圖①中m的值為
(2)求統計的這組銷售額額數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們學習了四邊形和一些特殊的四邊形,如圖表示了在某種條件下它們之間的關系.如果①,②兩個條件分別是:①兩組對邊分別平行;②有且只有一組對邊平行.那么請你對標上的其他6個數字序號寫出相對應的條件. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:①a一定是一個正數;②圓柱的上下兩底面是大小相等的圓,側面是平面;③棱柱的各條棱都相等;④幾個有理數的積等于0,那么其中至少有一個因數為0,其中正確的個數有( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.圓內接正六邊形的邊長與該圓的半徑相等
B.在平面直角坐標系中,不同的坐標可以表示同一點
C.一元二次方程ax2+bx+c=0(a≠0)一定有實數根
D.將△ABC繞A點按順時針方向旋轉60°得△ADE,則△ABC與△ADE不全等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
在平面直角坐標系xOy中,點P(x0,y0)到直線Ax+By+C=0的距離公式為:d=![]() .
.
例如:求點P0(0,0)到直線4x+3y﹣3=0的距離.
解:由直線4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴點P0(0,0)到直線4x+3y﹣3=0的距離為d=![]() =
=![]() .
.
根據以上材料,解決下列問題:
問題1:點P1(3,4)到直線y=﹣![]() x+
x+![]() 的距離為 ;
的距離為 ;
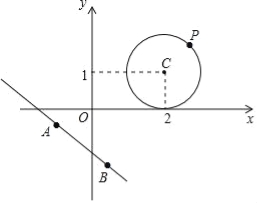
問題2:已知:⊙C是以點C(2,1)為圓心,1為半徑的圓,⊙C與直線y=﹣![]() x+b相切,求實數b的值;
x+b相切,求實數b的值;
問題3:如圖,設點P為問題2中⊙C上的任意一點,點A,B為直線3x+4y+5=0上的兩點,且AB=2,請求出S△ABP的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com