
【題目】如圖,在△ABC中,AB=AC=4,BC=2,點P、E、F分別為邊BC、AB、AC上的任意點,則PE+PF的最小值是_____.
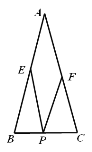
【答案】![]()
【解析】
當PE⊥AB,PF⊥AC時,PE+PF的值最小.
解:如圖,作CG⊥AB于G,PH⊥CG于H,
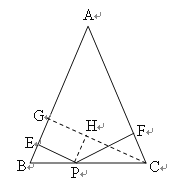
當PE⊥AB,PF⊥AC時,則∠EGH=GHP=∠PEG=90°,
∴四邊形PEGH為矩形,
∴PE=HG,PH∥AB,
∴∠B=∠HPC,
∵AB=AC,
∴∠B=∠FCP,
∴∠HPC=∠FCP,
∵∠PHC=∠CFP=90°,PC=CP,
∴△PHC≌△CFP(AAS),
∴CH=PF
∴PE+PF=HG+CH=CG,
故此時PE+PF將取得最小值.
在Rt△ACG中,
∵AC=4,
∴CG2=AC2-AG2=42-AG2,
在Rt△BCG中,
∵BC=2,BG=AB-AG=4-AG,
∴CG2=BC2-BG2=22-(4-AG)2,
∴42-AG2=22-(4-AG)2,
∴AG=![]() ,
,
∴CG=![]() =
=![]() =
=![]() ,
,
∴PE+PF=![]() ,
,
即PE+PF的最小值為![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】正方形ABCD的邊長為12,在其角上去掉兩個全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH頂點分別在正方形ABCD的邊上,且EH過N點,則正方形EFGH的邊長是( )
A.10
B.3 ![]()
C.4 ![]()
D.3 ![]() 或4
或4 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是過點
是過點![]() 的直線,
的直線,![]() 于
于![]() ,
,![]() 于點
于點![]() ;
;
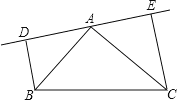
(1)若![]() 、
、![]() 在
在![]() 的同側(如圖所示)且
的同側(如圖所示)且![]() .求證:
.求證:![]() ;
;
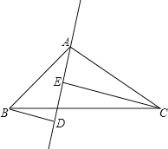
(2)若![]() 、
、![]() 在
在![]() 的兩側(如圖所示),且
的兩側(如圖所示),且![]() ,其他條件不變,
,其他條件不變,![]() 與
與![]() 仍垂直嗎?若是請給出證明;若不是,請說明理由.
仍垂直嗎?若是請給出證明;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,工人師傅常用“卡鉗”這種工具測定工件內槽的寬.卡鉗由兩根鋼條AA′、BB′組成,O為AA′、BB′的中點.只要量出A′B′的長度,由三角形全等就可以知道工件內槽AB的長度.則判定△OAB≌△OA′B′的依據是( )

A. SASB. ASAC. SSSD. AAS
查看答案和解析>>
科目:初中數學 來源: 題型:
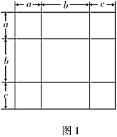
【題目】把幾個圖形拼成一個新的圖形,再通過圖形面積的計算,常常可以得到一些相關的代數等式,這些等式可用于代數式的證明或求一些不規則圖形的面積.
(1)如圖1,是將幾個面積不等的小正方形與小長方形拼成一個邊長為![]() 的正方形,若把這個大正方形的面積直接用邊長表示,其面積是________;若把這個大正方形的面積用分割成的小正方形或小矩形的面積表示時,其面積是________;無論怎樣表示,面積不變,所以,可得等式是________;并用多項式的乘法公式說明該等式成立;
的正方形,若把這個大正方形的面積直接用邊長表示,其面積是________;若把這個大正方形的面積用分割成的小正方形或小矩形的面積表示時,其面積是________;無論怎樣表示,面積不變,所以,可得等式是________;并用多項式的乘法公式說明該等式成立;
(2)已知三個數![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,
,![]() ,利用(1)中發現的結論可直接寫出
,利用(1)中發現的結論可直接寫出![]() ________;
________;
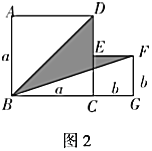
(3)如圖2,是將兩個邊長分別為![]() 和
和![]() 的正方形拼在一起,
的正方形拼在一起,![]() ,
,![]() ,
,![]() 三點在同一直線上,連接
三點在同一直線上,連接![]() 和
和![]() ,若兩正方形的邊長滿足
,若兩正方形的邊長滿足![]() ,
,![]() ,請求出陰影部分的面積.
,請求出陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖中,用數字表示的∠1、∠2、∠3、∠4各角中,錯誤的判斷是( )

A. 若將AC作為第三條直線,則∠1和∠3是同位角
B. 若將AC作為第三條直線,則∠2和∠4是內錯角
C. 若將BD作為第三條直線,則∠2和∠4是內錯角
D. 若將CD作為第三條直線,則∠3和∠4是同旁內角
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題6分)如圖,△ABC的頂點都在每個邊長為1個單位長度的方格紙的格點上,將△ABC向右平移3格,再向上平移2格.
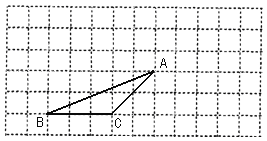
(1)請在圖中畫出平移后的![]() ;
;
(2)△ABC的面積為 _;
(3)若AB的長約為5.4,求出AB邊上的高(結果保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠CAB,交CB于點D,過點D作DE⊥AB于點E.
(1)求證:AC=AE;
(2)若點E為AB的中點,CD=4,求BE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com