
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() 與
與![]() 交于點
交于點 ![]() ,
,![]() 為
為![]() 延長線上的一點,且
延長線上的一點,且![]() ,連接
,連接![]() 分別交
分別交![]() ,
,![]() 于點
于點 ![]() ,
,![]() ,連接
,連接![]() ,則下列結論中一定成立的是__________.
,則下列結論中一定成立的是__________.
①![]() ;②與
;②與![]() 全等的三角形共有5個;③
全等的三角形共有5個;③![]() ;④由點
;④由點![]() 、
、![]() 、
、![]() 、
、![]() 構成的四邊形是菱形
構成的四邊形是菱形
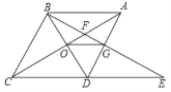
【答案】①④
【解析】
由AAS證明△ABG≌△DEG,得出AG=DG,證出OG是△ACD的中位線,得出OG=![]() CD=
CD=![]() AB,①正確;
AB,①正確;
先證明四邊形ABDE是平行四邊形,證出△ABD、△BCD是等邊三角形,得出AB=BD=AD,因此OD=AG,得出四邊形ABDE是菱形,④正確;
由菱形的性質得得出△ABG≌△BDG≌△DEG,由SAS證明△ABG≌△DCO,得出△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,得出②不正確;
證出OG是△ABD的中位線,得出OG∥AB,OG=![]() AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性質和面積關系得出S四邊形ODGF=S△ABF;③不正確;即可得出結果.
AB,得出△GOD∽△ABD,△ABF∽△OGF,由相似三角形的性質和面積關系得出S四邊形ODGF=S△ABF;③不正確;即可得出結果.
∵四邊形ABCD是菱形,
∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,
∵CD=DE,
∴AB=DE,
在△ABG和△DEG中,
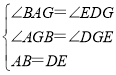 ,
,
∴△ABG≌△DEG(AAS),
∴AG=DG,
∴OG是△ACD的中位線,
∴OG=![]() CD=
CD=![]() AB,①正確;
AB,①正確;
∵AB∥CE,AB=DE,
∴四邊形ABDE是平行四邊形,
∵∠BCD=∠BAD=60°,
∴△ABD、△BCD是等邊三角形,
∴AB=BD=AD,∠ODC=60°,
∴OD=AG,四邊形ABDE是菱形,④正確;
∴AD⊥BE,
由菱形的性質得:△ABG≌△BDG≌△DEG,
在△ABG和△DCO中,
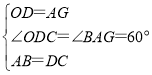 ,
,
∴△ABG≌△DCO(SAS),
∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正確;
∵OB=OD,AG=DG,
∴OG是△ABD的中位線,
∴OG∥AB,OG=![]() AB,
AB,
∴△GOD∽△ABD,△ABF∽△OGF,
∴△GOD的面積=![]() △ABD的面積,△ABF的面積=△OGF的面積的4倍,AF:OF=2:1,
△ABD的面積,△ABF的面積=△OGF的面積的4倍,AF:OF=2:1,
∴△AFG的面積=△OGF的面積的2倍,
又∵△GOD的面積=△AOG的面積=△BOG的面積,
∴S四邊形ODGF=S△ABF;③不正確;
正確的是①④.
故答案為:①④.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]()
![]() 經過原點和點
經過原點和點![]() ,頂點為
,頂點為![]() ,拋物線
,拋物線![]() 與拋物線
與拋物線![]() 關于原點
關于原點![]() 對稱.
對稱.
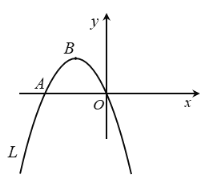
(1)求拋物線![]() 的函數表達式及點
的函數表達式及點![]() 的坐標;
的坐標;
(2)已知點![]() 、
、![]() 在拋物線
在拋物線![]() 上的對應點分別為
上的對應點分別為![]() 、
、![]() ,
,![]() 的對稱軸交
的對稱軸交![]() 軸于點
軸于點![]() ,則拋物線
,則拋物線![]() 的對稱軸上是否存在點
的對稱軸上是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() 點
點![]() 從點
從點![]() 出發以
出發以![]() 的速度沿折線
的速度沿折線![]() 運動,點
運動,點![]() 從點
從點![]() 出發以
出發以![]() 的速度沿
的速度沿![]() 運動,
運動,![]() 兩點同時出發,當某一點運動到點
兩點同時出發,當某一點運動到點![]() 時,兩點同時停止運動設運動時間為
時,兩點同時停止運動設運動時間為![]() 的面積為
的面積為![]() 關于
關于![]() 的函數圖像由
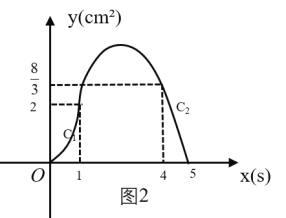
的函數圖像由![]() 兩段組成,如圖2所示.
兩段組成,如圖2所示.
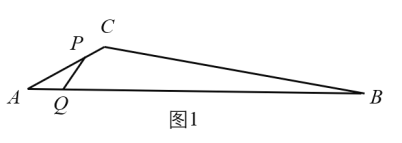
(1)求![]() 的值;
的值;
(2)求圖2中圖像![]() 段的函數表達式;
段的函數表達式;
(3)當點![]() 運動到線段
運動到線段![]() 上某一段時,
上某一段時,![]() 的面積大于當點
的面積大于當點![]() 在線段
在線段![]() 上任意一點時
上任意一點時![]() 的面積,求
的面積,求![]() 的取值范圍.(直接寫出答案)
的取值范圍.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“普洱茶”是云南有名的特產,某網店專門銷售某種品牌的普洱茶,成本為30元/盒,每天銷售![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間存在一次函數關系,如圖所示.
(元)之間存在一次函數關系,如圖所示.
(1)求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)如果規定每天該種普洱茶的銷售量不低于240盒,該網店店主熱心公益事業,決定從每天的銷售利潤中捐出500元給扶貧基金會,當銷售單價為多少元時,每天獲取的凈利潤最大,最大凈利潤是多少?(注:凈利潤=總利潤-捐款)
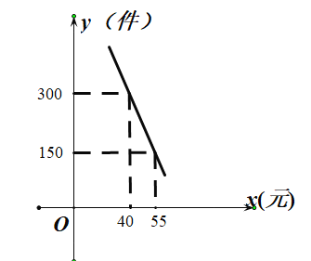
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】書法是我國的文化瑰寶,研習書法能培養高雅的品格某校為加強書法教學,了解學生現有的書寫能力,隨機抽取了部分學生進行測試,測試結果分為優秀、良好、及格、不及格四個等級,分別用![]() ,
,![]() ,
,![]() ,
,![]() 表示,并將測試結果繪制成如下兩幅不完整的統計圖.
表示,并將測試結果繪制成如下兩幅不完整的統計圖.
書寫能力等級測試條形統計圖:
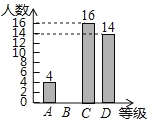
書寫能力等級測試扇形統計圖:
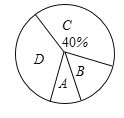
請根據統計圖中的信息解答以下問題:
(1)本次抽取的學生共有______人,扇形統計圖中![]() 所對應扇形的圓心角是_______
所對應扇形的圓心角是_______![]() ;
;
(2)把條形統計圖補充完整;
(3)依次將優秀、良好、及格、不及格記為![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,則抽取的這部分學生書寫成績的眾數是_______,中位數是_______,平均數是________;
分,則抽取的這部分學生書寫成績的眾數是_______,中位數是_______,平均數是________;
(4)若該校共有學生![]() 人,請估計一下,書寫能力等級達到優秀的學生大約有多少人?
人,請估計一下,書寫能力等級達到優秀的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的與
的與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
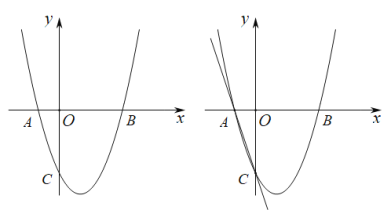
(1)求該拋物線的解析式及頂點的坐標;
(2)若![]() 是線段
是線段![]() 上一動點,過
上一動點,過![]() 作
作![]() 軸的平行線交拋物線于點
軸的平行線交拋物線于點![]() ,交
,交![]() 于點
于點![]() ,設
,設![]() 時,
時,![]() 的面積為
的面積為![]() .求
.求![]() 關于
關于![]() 的函數關系式;若
的函數關系式;若![]() 有最大值,請求出
有最大值,請求出![]() 的最大值,若沒有,請說明理由;
的最大值,若沒有,請說明理由;
(3)若![]() 是
是![]() 軸上一個動點,過
軸上一個動點,過![]() 作射線
作射線![]() 交拋物線于點
交拋物線于點![]() ,隨著
,隨著![]() 點的運動,在
點的運動,在![]() 軸上是否存在這樣的點
軸上是否存在這樣的點![]() ,使以
,使以 ![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,請直接寫出
為頂點的四邊形為平行四邊形?若存在,請直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
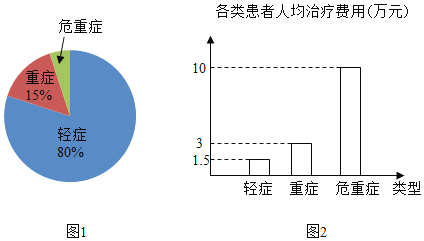
【題目】今年2﹣4月某市出現了200名新冠肺炎患者,市委根據黨中央的決定,對患者進行了免費治療.圖1是該市輕癥、重癥、危重癥三類患者的人數分布統計圖(不完整),圖2是這三類患者的人均治療費用統計圖.請回答下列問題.
(1)輕癥患者的人數是多少?
(2)該市為治療危重癥患者共花費多少萬元?
(3)所有患者的平均治療費用是多少萬元?
(4)由于部分輕癥患者康復出院,為減少病房擁擠,擬對某病房中的A、B、C、D、E五位患者任選兩位轉入另一病房,請用樹狀圖法或列表法求出恰好選中B、D兩位患者的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
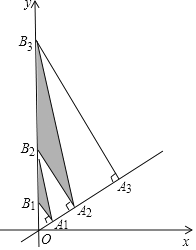
【題目】如圖,直線![]() 上有點
上有點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別過點
分別過點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 作直線
作直線![]() 的垂線,交
的垂線,交![]() 軸于點
軸于點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,依次連接
,依次連接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,得到
,得到![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() 的面積為_______.(用含有正整數
的面積為_______.(用含有正整數![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:在平面直角坐標系中,O為坐標原點,設點P的坐標為(x,y),當x<0時,點P的變換點P′的坐標為(﹣x,y);當x≥0時,點P的變換點P′的坐標為(﹣y,x).
(1)若點A(2,1)的變換點A′在反比例函數y=![]() 的圖象上,則k= ;
的圖象上,則k= ;
(2)若點B(2,4)和它的變換點B'在直線y=ax+b上,則這條直線對應的函數關系式為 ,∠BOB′的大小是 度.
(3)點P在拋物線y=x2﹣2x﹣3的圖象上,以線段PP′為對角線作正方形PMP'N,設點P的橫坐標為m,當正方形PMP′N的對角線垂直于x軸時,求m的取值范圍.
(4)拋物線y=(x﹣2)2+n與x軸交于點C,D(點C在點D的左側),頂點為E,點P在該拋物線上.若點P的變換點P′在拋物線的對稱軸上,且四邊形ECP′D是菱形,求n的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com