
【題目】計算下列各題
(1)計算:4sin60°﹣|3﹣ ![]() |+(
|+( ![]() )﹣2;
)﹣2;
(2)解方程:x2﹣ ![]() x﹣
x﹣ ![]() =0.
=0.
【答案】
(1)解:原式=2 ![]() ﹣2
﹣2 ![]() +3+4
+3+4
=7
(2)解:方法一:移項,得x2﹣ ![]() x=
x= ![]() ,
,
配方,得(x﹣ ![]() )2=1
)2=1
由此可得x﹣ ![]() =±1,
=±1,
x1=1+ ![]() ,x2=﹣1+
,x2=﹣1+ ![]()
方法二:a=1,b=﹣ ![]() ,c=﹣
,c=﹣ ![]() .
.
△=b2﹣4ac=(﹣ ![]() )2﹣4×1×(﹣
)2﹣4×1×(﹣ ![]() )=4>0
)=4>0
方程有兩個不等的實數根
x= ![]() =
= ![]() =
= ![]() ±1,
±1,
x1=1+ ![]() ,x2=﹣1+
,x2=﹣1+ ![]()
【解析】(1)本題涉及負整數指數冪、二次根式化簡、絕對值、特殊角的三角函數值四個考點.針對每個考點分別進行計算,然后根據實數的運算法則求得計算結果;(2)利用配方法或公式法解答此題,均可得結果.
【考點精析】本題主要考查了整數指數冪的運算性質和特殊角的三角函數值的相關知識點,需要掌握aman=am+n(m、n是正整數);(am)n=amn(m、n是正整數);(ab)n=anbn(n是正整數);am/an=am-n(a不等于0,m、n為正整數);(a/b)n=an/bn(n為正整數);分母口訣:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口訣:“123,321,三九二十七”才能正確解答此題.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在以O為圓心的兩個同心圓中,小圓的半徑為1,AB與小圓相切于點A,與大圓相交于點B,大圓的弦BC⊥AB于點B,過點C作大圓的切線CD交AB的延長線于點D,連接OC交小圓于點E,連接BE、BO. 
(1)求證:△AOB∽△BDC;
(2)設大圓的半徑為x,CD的長為y: ①求y與x之間的函數關系式;
②當BE與小圓相切時,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等腰直角三角形,∠A=90°,BC=4,點P是△ABC邊上一動點,沿B→A→C的路徑移動,過點P作PD⊥BC于點D,設BD=x,△BDP的面積為y,則下列能大致反映y與x函數關系的圖象是( )
A.
B.
C.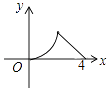
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是矩形,對角線AC的垂直平分線交AD于點E,交BC于點F,連接AF,CE,解答下列問題: 
(1)求證:四邊形AECF是菱形;
(2)記AB=a,BF=b,若a,b是方程x2﹣2(m+1)x+m2+1=0的兩根,問當m為何值時,菱形AECF的周長為8 ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=5,BC=6,將△ABC繞點C順時針方向旋轉一定角度后得到△A′B′C.若點A′恰好落在BC的延長線上,則點B′到BA′的距離為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑作半圓⊙O,交BC于點D,連接AD,過點D作DE⊥AC,垂足為點E,交AB的延長線于點F. 
(1)求證:EF是⊙0的切線.
(2)如果⊙0的半徑為5,sin∠ADE= ![]() ,求BF的長.
,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合,展開后,折痕DE分別交AB,AC于點E、G,連接GF,有下列結論: ①∠AGD=112.5°;②tan∠AED= ![]() +1;③四邊形AEFG是菱形;④S△ACD=
+1;③四邊形AEFG是菱形;④S△ACD= ![]() S△OCD .
S△OCD .
其中正確結論的序號是 . (把所有正確結論的序號都填在橫線上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△AOB中,∠AOB為直角,OA=6,OB=8,半徑為2的動圓圓心Q從點O出發,沿著OA方向以1個單位長度/秒的速度勻速運動,同時動點P從點A出發,沿著AB方向也以1個單位長度/秒的速度勻速運動,設運動時間為t秒(0<t≤5)以P為圓心,PA長為半徑的⊙P與AB、OA的另一個交點分別為C、D,連結CD、QC.
(1)當t為何值時,點Q與點D重合?
(2)當⊙Q經過點A時,求⊙P被OB截得的弦長.
(3)若⊙P與線段QC只有一個公共點,求t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知反比例函數y= ![]() (x>0)的圖象和菱形OABC,且OB=4,tan∠BOC=
(x>0)的圖象和菱形OABC,且OB=4,tan∠BOC= ![]() .
. 
(1)求A、B、C三點的坐標;
(2)若將菱形向右平移,菱形的兩個頂點恰好同時落在反比例函數的圖象上,猜想這是哪兩個點,并求菱形的平移距離和反比例函數的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com