分析:由于△OP1A1是等腰直角三角形,過點P1作P1M⊥x軸,則P1M=OM=MA1,所以可設P1的坐標是(a,a),把(a,a)代入解析式得到a=4,從而求出A1的坐標是(8,0),再根據△P2A1A2是等腰直角三角形,設P2的縱坐標是b,則P2的橫坐標是8+b,把(8+b,b)代入函數解析式得到b的值,故可得出A2的橫坐標,同理可以得到A3,An的橫坐標,根據等腰三角形的性質得到y1+y2+…yn等于An點橫坐標的一半即可得出結論.
解答: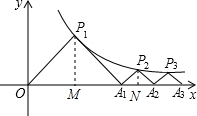
解:如圖,過點P
1作P
1M⊥x軸,
∵△OP
1A
1是等腰直角三角形,
∴P
1M=OM=MA
1,
設P
1的坐標是(a,a),把(a,a)代入解析式y=
(x>0)中,得a=4,
∴A
1的坐標是(8,0),
又∵△P
2A
1A
2是等腰直角三角形,
∴設P
2的縱坐標是b,則P
2的橫坐標是8+b,把(8+b,b)代入函數解析式得b=
,
解得b=4
-4,
∴A
2的橫坐標是8+2b=8+8
-8=8
,
同理可以得到A
3的橫坐標是8
,A
n的橫坐標是8
,
根據等腰直角三角形的性質得到y
1+y
2+…y
10等于A
10點橫坐標的一半,
故y
1+y
2+…y
10=
×8
=4
.
故答案為:4
.
點評:本題考查的是反比例函數綜合題及等腰直角三角形的性質,根據題意作出輔助線,找出點P的橫坐標與縱坐標的關系是解答此題的關鍵.

 如圖所示,P1(x1,y1)、P2(x2,y2),…P10(x10,y10)在函數y=
如圖所示,P1(x1,y1)、P2(x2,y2),…P10(x10,y10)在函數y= 解:如圖,過點P1作P1M⊥x軸,
解:如圖,過點P1作P1M⊥x軸,

 名校課堂系列答案
名校課堂系列答案 如圖所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函數y=
如圖所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函數y= 如圖所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函數y=
如圖所示,P1(x1,y1)、P2(x2,y2),…Pn(xn,yn)在函數y= 的圖象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜邊OA1,A1A2……An-1An,都在x軸上, 則y1+y2+…yn= 。
的圖象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜邊OA1,A1A2……An-1An,都在x軸上, 則y1+y2+…yn= 。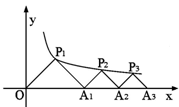
 (x>0)的圖象上,△OP1A1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜邊OA1,
(x>0)的圖象上,△OP1A1,△P2A1A2,△P3A2A3…△PnAn-1An…都是等腰直角三角形,斜邊OA1,