
【題目】已知關于x的方程![]() 有兩個正整數根
有兩個正整數根![]() 是正整數
是正整數![]() 的三邊a、b、c滿足
的三邊a、b、c滿足![]() ,
,![]() ,
,![]() .
.
求:![]() 的值;
的值;
![]() 的面積.
的面積.
【答案】![]() m=2
m=2![]() 1或
1或![]()
【解析】
(1)本題可先求出方程(m2-1)x2-3(3m-1)x+18=0的兩個根,然后根據這兩個根都是正整數求出m的值.
(2)由(1)得出的m的值,然后將m2+a2m-8a=0,m2+b2m-8b=0.進行化簡,得出a,b的值.然后再根據三角形三邊的關系來確定符合條件的a,b的值,進而得出三角形的面積.
![]() 關于x的方程
關于x的方程![]() 有兩個正整數根
有兩個正整數根![]() 是整數
是整數![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
設![]() ,
,![]() 是此方程的兩個根,
是此方程的兩個根,
![]() ,
,
![]() 也是正整數,即
也是正整數,即![]() 或2或3或6或9或18,
或2或3或6或9或18,
又m為正整數,
![]() ;
;
![]() 把
把![]() 代入兩等式,化簡得
代入兩等式,化簡得![]() ,
,![]()
當![]() 時,
時,![]()
當![]() 時,a、b是方程
時,a、b是方程![]() 的兩根,而
的兩根,而![]() ,由韋達定理得
,由韋達定理得![]() ,
,![]() ,則
,則![]() 、
、![]() .
.
![]() ,
,![]() 時,由于
時,由于![]()
故![]() 為直角三角形,且
為直角三角形,且![]() ,
,![]() .
.
![]() ,
,![]() 時,因
時,因![]() ,故不能構成三角形,不合題意,舍去.
,故不能構成三角形,不合題意,舍去.
![]() ,
,![]() 時,因
時,因![]() ,故能構成三角形.
,故能構成三角形.
![]()
綜上,![]() 的面積為1或
的面積為1或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】武漢市光谷實驗中學九(1)班為了了解全班學生喜歡球類活動的情況,采取全面調查的方法,從足球、乒乓球、籃球、排球等四個方面調查了全班學生的興趣愛好,根據調查的結果組建了4個興趣小組,并繪制成如圖所示的兩幅不完整的統計圖(如圖①,②,要求每位學生只能選擇一種自己喜歡的球類),下列說法錯誤的是( )

A. 九(1)班的學生人數為40 B. m的值為10
C. n的值為20 D. 表示“足球”的扇形的圓心角是70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(1,0),以線段OA為邊在第四象限內作等邊三角形AOB,點C為x正半軸上一動點(OC>1),連接BC,以線段BC為邊在第四象限內作等邊△CBD,連接DA并延長,交y軸于點E.
①△OBC與△ABD全等嗎?判斷并證明你的結論;
②當點C運動到什么位置時,以A,E,C為頂點的三角形是等腰三角形?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支持四川抗震救災,重慶市A、B、C三地現在分別有賑災物資100噸、100噸、80噸,需要全部運往四川重災地區的D、E兩縣.根據災區的情況,這批賑災物資運往D縣的數量比運往E縣的數量的2倍少20噸.
(1)求這批賑災物資運往D、E兩縣的數量各是多少?
(2)若要求C地運往D縣的賑災物資為60噸,A地運往D的賑災物資為x噸(x為整數),B地運往D縣的賑災物資數量小于A地運往D縣的賑災物資數量的2倍.其余的賑災物資全部運往E縣,且B地運往E縣的賑災物資數量不超過25噸.則A、B兩地的賑災物資運往D、E兩縣的方案有幾種?請你寫出具體的運送方案;
(3)已知A、B、C三地的賑災物資運往D、E兩縣的費用如下表:
A地 | B地 | C地 | |
運往D縣的費用(元/噸) | 220 | 200 | 200 |
運往E縣的費用(元/噸) | 250 | 220 | 210 |
為及時將這批賑災物資運往D、E兩縣,某公司主動承擔運送這批賑災物資的總費用,在(2)問的要求下,該公司承擔運送這批賑災物資的總費用最多是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() ,
,![]() 于R,
于R,![]() 于S,則四個結論正確的是
于S,則四個結論正確的是![]()
![]()
![]() 點P在
點P在![]() 的平分線上;
的平分線上;
![]() ;
;
![]() ;
;
![]() ≌
≌![]() .
.
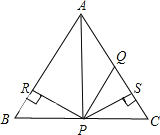
A. 全部正確 B. 僅![]() 和
和![]() 正確 C. 僅
正確 C. 僅![]() 正確 D. 僅
正確 D. 僅![]() 和
和![]() 正確
正確
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是以原點為圓心, ![]() 為半徑的圓,點P是直線y=﹣x+6上的一點,過點P作⊙O的一條切線PQ,Q為切點,則切線長PQ的最小值為( )
為半徑的圓,點P是直線y=﹣x+6上的一點,過點P作⊙O的一條切線PQ,Q為切點,則切線長PQ的最小值為( )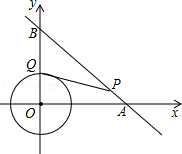
A.3
B.4
C.6﹣ ![]()
D.3 ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=6,BC=8,點F在邊AC上,并且CF=2,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是 . 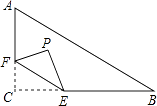
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列兩個等式:3+2=3×2﹣1,4+![]() =4×
=4×![]() ﹣1,給出定義如下:
﹣1,給出定義如下:
我們稱使等式a+b=ab﹣1成立的一對有理數a,b為“椒江有理數對”,記為(a,b),如:數對(3,2),(4,![]() )都是“椒江有理數對”.
)都是“椒江有理數對”.
(1)數對(﹣2,1),(5,![]() )中是“椒江有理數對”的是 ;
)中是“椒江有理數對”的是 ;
(2)若(a,3)是“椒江有理數對”,求a的值;
(3)若(m,n)是“椒江有理數對”,則(﹣n,﹣m) “椒江有理數對”(填“是”、“不是”或“不確定”).
(4)請再寫出一對符合條件的“椒江有理數對”
(注意:不能與題目中已有的“椒江有理數對”重復)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延長CA至點E,使AE=AC;延長CB至點F,使BF=BC.連接AD,AF,DF,EF.延長DB交EF于點N. 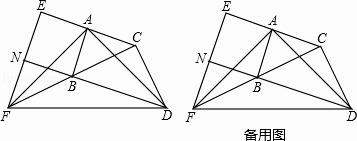
(1)求證:AD=AF;
(2)求證:BD=EF;
(3)試判斷四邊形ABNE的形狀,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com