【題目】如圖，在△ABC中，AD是高，AE是∠BAC的平分線，AF是BC邊上的中線，則下列線段中，最短的是（ ）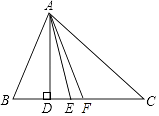 
A.AB
B.AE
C.AD
D.AF
【答案】C
【解析】解：∵在△ABC中，AD是高， ∴AD⊥BC，
又∵在△ABC中，AE是∠BAC的平分線，AF是BC邊上的中線，
∴AD＜AB，AD＜AE，AD＜AF，
故選C．
【考點精析】根據題目的已知條件，利用垂線段最短和三角形的“三線”的相關知識可以得到問題的答案，需要掌握連接直線外一點與直線上各點的所有線段中，垂線段最短；現實生活中開溝引水，牽牛喝水都是“垂線段最短”性質的應用；1、三角形角平分線的三條角平分線交于一點(交點在三角形內部，是三角形內切圓的圓心，稱為內心);2、三角形中線的三條中線線交于一點(交點在三角形內部，是三角形的幾何中心，稱為中心);3、三角形的高線是頂點到對邊的距離；注意：三角形的中線和角平分線都在三角形內．
云南師大附小一線名師提優作業系列答案科目：初中數學 來源： 題型：
【題目】有這樣一個問題：探究函數
的圖象與性質．
小華根據學習函數的經驗，對函數
的圖象與性質進行了探究.下面是小華的探究過程,請補充完整:
(1)函數
的自變量x的取值范圍是 ；
(2)下表是y與x的幾組對應值.
x | … | -3 | -2 | -1 | 0 |
| 1 | 3 |
| 4 | 5 | 6 | 7 | … |
y | … |
|
|
|
|
| 6 | 6 |
|
|
|
| m | … |
求m的值；
（3）如下圖，在平面直角坐標系xOy中，描出了以上表中各對對應值為坐標的點.根據描出的點，畫出該函數的圖象；
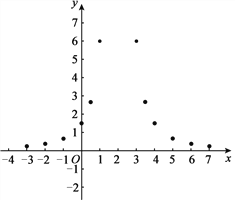
（4）結合函數的圖象，寫出該函數的一條性質： .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面的證明（下劃線內補全證明過程，括號內填寫推理的依據）．
（1）如圖1，AB∥CD，∠B+∠D=180°，求證：CB∥DE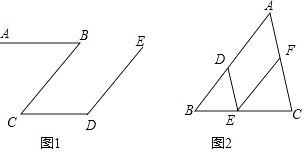 
證明：∵AB∥CD（已知）
∴∠B=
∵∠B+∠D=180°（已知）
∴∠C+∠D=180°（等量代換）
∴∥
（2）如圖2，已知DE∥AC，∠A=∠DEF，請證明∠B=∠FEC． 證明：∵DE∥AC（已知）
∴∠A=
∵∠A=∠DEF（已知）
∴∠DEF=∠（等量代換）
∴AB∥
∴∠=∠ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A，B坐標分別為A（0，a），B（b，a），且實數a，b滿足（a﹣3）2+|b﹣5|=0，現同時將點A，B分別向下平移3個單位，再向左平移1個單位，分別得到點A，B的對應點C，D，連接AC，BD，AB．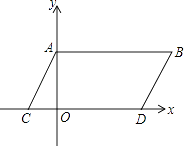 
（1）求點C，D的坐標及四邊形ABDC的面積；
（2）在y軸上是否存在一點M，連接MC，MD，使S△MCD=S四邊形ABDC？若存在這樣一點，求出點M的坐標；若不存在，試說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
