【題目】以下是通過折疊正方形紙片得到等邊三角形的步驟取一張正方形的紙片進行折疊，具體操作過程如下：
第一步：如圖，先把正方形ABCD對折，折痕為MN；
第二步：點E在線段MD上，將△ECD沿EC翻折，點D恰好落在MN上，記為點P，連接BP可得△BCP是等邊三角形
問題：在折疊過程中，可以得到PB=PC；依據是________________________.
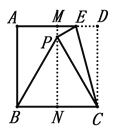
鷹派教輔銜接教材河北教育出版社系列答案
初中暑期銜接系列答案科目：初中數學 來源： 題型：
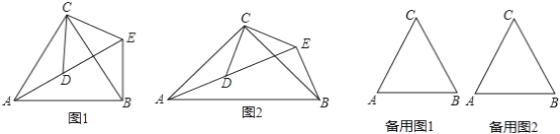
【題目】（1）問題發現：如圖1，△ACB和△DCE均為等邊三角形，當△DCE旋轉至點A，D，E在同一直線上，連接BE．
填空：① ∠AEB的度數為_______；②線段AD、BE之間的數量關系是______．
（2）拓展研究：
如圖2，△ACB和△DCE均為等腰三角形，且∠ACB=∠DCE=90°，點A、D、E在同一直線上，若AE=15，DE=7，求AB的長度．
（3）探究發現：
圖1中的△ACB和△DCE，在△DCE旋轉過程中當點A，D，E不在同一直線上時，設直線AD與BE相交于點O，試在備用圖中探索∠AOE的度數，直接寫出結果，不必說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，數軸上有兩定點A、B，點
表示的數為6，點B在點A的左側，且AB=20，動點P從點A出發，以每秒4個單位長度的速度沿數軸向左勻速運動，設運動時間為t秒（t>0）.
（1）寫出數軸上點B表示的數______，點P表示的數用含t的式子表示：_______；
（2）設點M是AP的中點，點N是PB的中點.點P在直線AB上運動的過程中，線段MN的長度是否會發生變化？若發生變化，請說明理由；若不變化，求出線段MN的長度.
（3）動點R從點B出發，以每秒2個單位長度的速度沿數軸向左勻速運動，若點P、R同時出發；當點P運動多少秒時？與點R的距離為2個單位長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們規定:若關于
的一元一次方程
的解為
，則稱該方程為“和解方程”．例如:方程
的解為
，而
， 則方程為“和解方程"．請根據上述規定解答下列問題:(1)已知關于的一元一次方程
是“和解方程”，則
的值為________．(2)己知關于的一元一次方程
是“和解方程”，并且它的解是
，則
的值為_________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：
材料1、若一元二次方程ax2+bx+c=0（a≠0）的兩根為x1，x2，則x1+x2=
，x1x2=
．
材料2、已知實數m、n滿足m2﹣m﹣1=0，n2﹣n﹣1=0，且m≠n，求
的值．
解：由題知m、n是方程x2﹣x﹣1=0的兩個不相等的實數根，根據材料1得
m+n=1，mn=﹣1
∴
根據上述材料解決下面問題；
（1）一元二次方程2x2+3x﹣1=0的兩根為x1、x2，則x1+x2= ，x1x2= ．
（2）已知實數m、n滿足2m2﹣2m﹣1=0，2n2﹣2n﹣1=0，且m≠n，求m2n+mn2的值．
（3）已知實數p、q滿足p2=3p+2，2q2=3q+1，且p≠2q，求p2+4q2的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，已知矩形ABED，點C是邊DE的中點，且AB=2AD.
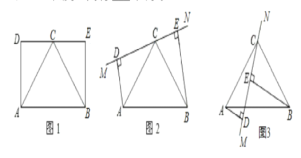
(1)由圖1通過觀察、猜想可以得到線段AC與線段BC的數量關系為___，位置關系為__；
(2)保持圖1中的△ABC固定不變,繞點C旋轉DE所在的直線MN到圖2中的位置(當垂線AD、BE在直線MN的同側).試探究線段AD、BE、DE長度之間有什么關系?并給予證明(第一問中得到的猜想結論可以直接在證明中使用)；
(3)保持圖2中的△ABC固定不變,繼續繞點C旋轉DE所在的直線MN到圖3中的位置(當垂線段AD、BE在直線MN的異側).試探究線段AD、BE、DE長度之間有___關系.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，有一拋物線其表達式為
.
（1）當該拋物線過原點時，求
的值；
（2）坐標系內有一矩形OABC,其中
、
.
①直接寫出C點坐標；
②如果拋物線與該矩形有2個交點，求的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我市晶泰星公司安排
名工人生產甲、乙兩種產品，每人每天生產
件甲產品或
件乙產品.根據市場行情測得，甲產品每件可獲利
元，乙產品每件可獲利
元.而實際生產中，生產乙產品需要數外支出一定的費用，經過核算，每生產件乙產品，當天每件乙產品平均荻利減少元，設每天安排
人生產乙產品.
(1)根據信息填表：
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 |
| ||
乙 |
|
|
(2)若每天生產甲產品可獲得的利潤比生產乙產品可獲得的利潤多
元，試問：該企業每天生產甲、乙產品可獲得總利潤是多少元?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】七年級一班和二班各推選
名同學進行投籃比賽，按照比賽規則，每人各投了個球，兩個班選手的進球數統計如下表，請根據表中數據回答問題．
進球數（個） |
|
|
|
|
|
|
一班人數（人） |
|
|
|
|
|
|
二班人數（人） |
|
|
|
|
|
|
填表；
平均數 | 中位數 | 眾數 | 方差 | |
一班 | 2.6 | |||
二班 | 7 | 7 | 7 |
如果要從這兩個班中選出一個班代表級部參加學校的投籃比賽，爭取奪得總進球數團體第一名，你認為應該選擇哪個班？如果要爭取個人進球數進入學校前三名，你認為應該選擇哪個班？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
