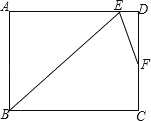
【題目】(2016廣西省賀州市第18題)在矩形ABCD中，∠B的角平分線BE與AD交于點E，∠BED的角平分線EF與DC交于點F，若AB=9，DF=2FC，則BC= ．（結果保留根號）
【答案】6
+3
【解析】
試題分析：先延長EF和BC，交于點G，再根據條件可以判斷三角形ABE為等腰直角三角形，并求得其斜邊BE的長，然后根據條件判斷三角形BEG為等腰三角形，最后根據△EFD∽△GFC得出CG與DE的倍數關系，并根據BG=BC+CG進行計算即可．延長EF和BC，交于點G
∵矩形ABCD中，∠B的角平分線BE與AD交于點E，∴∠ABE=∠AEB=45°，∴AB=AE=9，
∴直角三角形ABE中，BE=
=
，又∵∠BED的角平分線EF與DC交于點F，∴∠BEG=∠DEF
∵AD∥BC∴∠G=∠DEF∴∠BEG=∠G∴BG=BE=
由∠G=∠DEF，∠EFD=∠GFC，可得△EFD∽△GFC∴
設CG=x，DE=2x，則AD=9+2x=BC ∵BG=BC+CG ∴=9+2x+x 解得x=
∴BC=9+2（﹣3）=
小學課時特訓系列答案科目：初中數學 來源： 題型：
【題目】下列判斷正確的是（ ）
A.四條邊相等的四邊形是正方形B.四個角相等的四邊形是矩形
C.對角線垂直的四邊形是菱形D.對角線相等的四邊形是平行四邊形
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,已知點C在線段AB上,線段AC=6厘米,BC=4厘米,點M,N分別是AC,BC的中點.
(1)求線段MN的長度;
(2)根據第(1)題的計算過程和結果,設AC+BC=a,其他條件不變,你能猜出MN的長度嗎?請用一句話表述你發現的規律.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了探究n條直線能把平面最多分成幾部分,我們從最簡單的情形入手.
(1)一條直線把平面分成2部分;
(2)兩條直線最多可把平面分成4部分;
(3)三條直線最多可把平面分成7部分…
把上述探究的結果進行整理,列表如下:
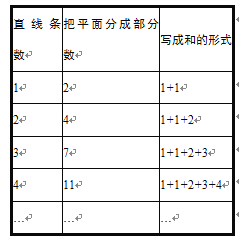
(1)當直線條數為5時,把平面最多分成 部分,寫成和的形式為 ;
(2)當直線條數為10時,把平面最多分成 部分;
(3)當直線條數為n時,把平面最多分成幾部分?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】景區大樓AB段上有四處居民小區A，B，C，D，且有AC=CD=DB，為改善居民購物的環境，要在AB路建一家超市，每個小區的居民各執一詞，難以確定超市的位置，如果由你出任超市負責人，以便民、獲利的角度考慮，你將把超市建在哪兒？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
