
【題目】某中學決定在本校學生中開展足球、籃球、羽毛球、乒乓球四種活動,為了了解學生對這四種活動的喜愛情況,學校隨機調查了該校m名學生,看他們喜愛哪一種活動(每名學生必選一種且只能從這四種活動中選擇一種),現將調查的結果繪制成如下不完整的統計圖.請你根據圖中的信息,解答下列問題.

(1)m= ,n= ;
(2)請補全圖中的條形圖;
(3)扇形統計圖中,足球部分的圓心角是 度;
(4)根據抽樣調查的結果,請估算全校1800名學生中,大約有多少人喜愛踢足球.
【答案】(1) 100,15 (2)見解析 (3)144° (4)720人
【解析】分析:(1)根據喜愛乒乓球的有10人,占10%可以求得m的值,從而可以求得n的值;
(2)根據題意和m的值可以求得喜愛籃球的人數,從而可以將條形統計圖補充完整;
(3)根據統計圖中的數據可以得到足球部分的百分比,即可得到足球部分的圓心角度數;
(4)根據統計圖中的數據可以估算出全校1800名學生中,大約有多少人喜愛踢足球;
詳解:(1)由題意可得:m=10÷10%=100,n%=15÷100=15%.
故答案為:100,15;
(2)喜愛籃球的有:100×35%=35(人),補全的條形統計圖,如圖所示:

(3)扇形統計圖中,足球部分的圓心角是360°×![]() =144°;
=144°;
故答案為:144;
(4)由題意可得:全校1800名學生中,喜愛踢足球的有:1800×![]() =720(人).
=720(人).
答:全校1800名學生中,大約有720人喜愛踢足球.


科目:初中數學 來源: 題型:
【題目】已知一個由正奇數排成的數陣.用如圖所示的四邊形框去框住四個數.

(1)若設框住四個數中左上角的數為n,則這四個數的和為 (用n的代數式表示);
(2)平行移動四邊形框,若框住四個數的和為228,求出這4個數;
(3)平行移動四邊形框,能否使框住四個數的和為508?若能,求出這4個數;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某淘寶店銷售A,B兩種商品,2018年8~12月每月銷售數量的情況如圖所示,在________月結束后,A![]() 商品的總銷售數量大于B
商品的總銷售數量大于B![]() 商品的總銷售數量.
商品的總銷售數量.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC與BD相交于點O,限用無刻度直尺完成以下作圖:
(1)在圖1中作線段BC的中點P;
(2)在圖2中,在OB、OC上分別取點E、F,使EF∥BC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動
問題情境:
如圖1,在ABC中,AB=AC,∠BAC=90°,D,E分別是邊AB,AC的中點,將ADE繞點A順時針旋轉α角(0°<α<90°)得到AD′E′,連接CE′,BD′.探究CE′與BD′的數量關系;
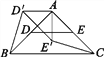 圖1
圖1 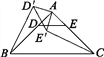 圖2
圖2 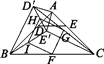 圖3
圖3 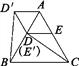 圖4
圖4
探究發現:
(1)圖1中,CE′與BD′的數量關系是________;
(2)如圖2,若將問題中的條件“D,E分別是邊AB,AC的中點”改為“D為AB邊上任意一點,DE∥BC交AC于點E”,其他條件不變,(1)中CE′與BD′的數量關系還成立嗎?請說明理由;
拓展延伸:
(3)如圖3,在(2)的條件下,連接BE′,CD′,分別取BC,CD′,E′D′,BE′的中點F,G,H,I,順次連接F,G,H,I得到四邊形FGHI.請判斷四邊形FGHI的形狀,并說明理由;
(4)如圖4,在ABC中,AB=AC,∠BAC=60°,點D,E分別在AB,AC上,且DE∥BC,將ADE繞點A順時針旋轉60°得到AD′E′,連接CE′,BD′.請你仔細觀察,提出一個你最關心的數學問題(例如:CE′與BD′相等嗎?).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,矩形OABC的頂點O、A、C的坐標分別為O(0,0),A(﹣x,0),C(0,y),且x、y滿足![]() .
.
(1)矩形的頂點B的坐標是 .
(2)若D是AB中點,沿DO折疊矩形OABC,使A點落在點E處,折痕為DO,連BE并延長BE交y軸于Q點.
①求證:四邊形DBOQ是平行四邊形.
②求△OEQ面積.
(3)如圖2,在(2)的條件下,若R在線段AB上,AR=4,P是AB左側一動點,且∠RPA=135°,求QP的最大值是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,有點![]() 、點
、點![]() .
.
(1)當A、B兩點關于x軸對稱時,求![]() 的面積;
的面積;
(2)若點A向上平移2個單位,再向右平移3個單位,得到點與點B重合,求A的坐標;
(3)當線段![]() 軸,且
軸,且![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
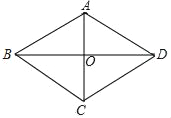
【題目】如圖所示,已知平行四邊形ABCD,對角線AC,BD相交于點O,∠BAO=∠DAO.
(1)求證:平行四邊形ABCD是菱形;
(2)請添加一個條件使菱形ABCD為正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,過點
,過點![]() 作
作![]() 平行于
平行于![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,過點
,過點![]() 作
作![]() 平行于
平行于![]() 軸,交直線
軸,交直線![]() 于點
于點![]() ,以
,以![]() 為邊長作等邊
為邊長作等邊![]() ,…,則等邊
,…,則等邊![]() 的邊長是______.
的邊長是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com