
【題目】為了加強對校內外安全監控,創建平安校園,某學校計劃增加15臺監控攝像設備,現有甲、乙兩種型號的設備,其中每臺價格,有效監控半徑如表所示,經調查,購買1臺甲型設備比購買1臺乙型設備多150元,購買2臺甲型設備比購買3臺乙型設備少400元.
甲型 | 乙型 | |
價格(元/臺) | a | b |
有效半徑(米/臺) | 150 | 100 |
(1)求a、b的值;
(2)若購買該批設備的資金不超過11000元,且要求監控半徑覆蓋范圍不低于1600米,兩種型號的設備均要至少買一臺,請你為學校設計購買方案,并計算最低購買費用.
【答案】(1)a=850,b=700;(2)最省錢的購買方案為:購甲型設備2臺,乙型設備13臺.
【解析】
(1)根據購買1臺甲型設備比購買1臺乙型設備多150元,購買2臺甲型設備比購買3臺乙型設備少400元,可列出方程組,解之即可得到a、b的值;
(2)可設購買甲型設備x臺,則購買乙型設備(15﹣x)臺,根據購買該批設備的資金不超過11000元、監控半徑覆蓋范圍不低于1600米,列出不等式組,根據x的值確定方案,然后對所需資金進行比較,并作出選擇.
解:(1)由題意得:![]() ,
,
解得![]() ;
;
(2)設購買甲型設備x臺,則購買乙型設備(15﹣x)臺,依題意得
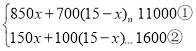 ,
,
解不等式①,得:x≤3![]() ,
,
解不等式②,得:x≥2,
則2≤x≤3![]() ,
,
∴x取值為2或3.
當x=2時,購買所需資金為:850×2+700×13=10800(元),
當x=3時,購買所需資金為:850×3+700×12=10950(元),
∴最省錢的購買方案為:購甲型設備2臺,乙型設備13臺.


科目:初中數學 來源: 題型:
【題目】已知一件文化衫價格為18元,一個書包的價格比一件文化衫價格的2倍還少6元.
(1)求一個書包的價格是多少元?
(2)某公司出資1 800元,拿出不少于350元但不超過400元的經費獎勵山區小學的優秀學生,剩余經費還能為多少名山區小學的學生每人購買一個書包和一件文化衫?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=a(x+3)(x﹣1)(a≠0),與x軸從左至右依次相交于A、B兩點,與y軸相交于點C,經過點A的直線y=﹣ ![]() x+b與拋物線的另一個交點為D.
x+b與拋物線的另一個交點為D.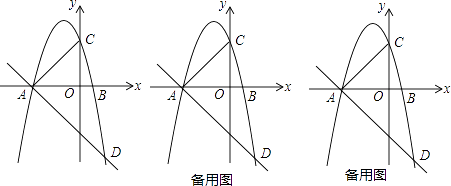
(1)若點D的橫坐標為2,求拋物線的函數解析式;
(2)若在第三象限內的拋物線上有點P,使得以A、B、P為頂點的三角形與△ABC相似,求點P的坐標;
(3)在(1)的條件下,設點E是線段AD上的一點(不含端點),連接BE.一動點Q從點B出發,沿線段BE以每秒1個單位的速度運動到點E,再沿線段ED以每秒 ![]() 個單位的速度運動到點D后停止,問當點E的坐標是多少時,點Q在整個運動過程中所用時間最少?
個單位的速度運動到點D后停止,問當點E的坐標是多少時,點Q在整個運動過程中所用時間最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形ABCD是以AB為直徑的⊙M的內接四邊形,點A,B在x軸上,△MBC是邊長為2的等邊三角形,過點M作直線l與x軸垂直,交⊙M于點E,垂足為點M,且點D平分 ![]() .
.
(1)求過A,B,E三點的拋物線的解析式;
(2)求證:四邊形AMCD是菱形;
(3)請問在拋物線上是否存在一點P,使得△ABP的面積等于定值5?若存在,請求出所有的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)四邊形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,點E在CD的延長線上,∠BAC=∠DAE.
(1)求證:△ABC≌△ADE;
(2)求證:CA平分∠BCD;
(3)如圖(2),設AF是△ABC的BC邊上的高,求證:EC=2AF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校食堂廚房的桌子上整齊地擺放著若干相同規格的碟子,碟子的個數與碟子的高度的關系如下表:
碟子的個數 | 碟子的高度(單位:cm) |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |

(1)當桌子上放有x(個)碟子時,請寫出此時碟子的高度(用含x的式子表示);
(2)分別從三個方向上看,其三視圖如上圖所示,廚房師傅想把它們整齊疊成一摞,求疊成一摞后的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,我們給中國象棋棋盤建立一個平面直角坐標系(每個小正方形的邊長均為![]() ),根據象棋中“馬”走“日”的規定,若“馬”的位置在圖中的點
),根據象棋中“馬”走“日”的規定,若“馬”的位置在圖中的點![]()
![]()
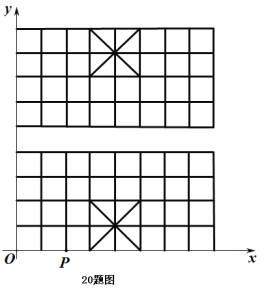
![]() 寫出下一步“馬”可能到達的點的坐標為_ (寫出所有可能的點的坐標);
寫出下一步“馬”可能到達的點的坐標為_ (寫出所有可能的點的坐標);
![]() 順次連接
順次連接![]() 中的所有點,得到的圖形是 _圖形(填“中心對稱”或“軸對稱”;
中的所有點,得到的圖形是 _圖形(填“中心對稱”或“軸對稱”;
![]() 將
將![]() 中得到的圖形各頂點的坐標都乘以
中得到的圖形各頂點的坐標都乘以![]() 請在平面直角坐標系中畫出變化后的圖形,并與原圖形比較,形狀和大小有怎樣的變化?
請在平面直角坐標系中畫出變化后的圖形,并與原圖形比較,形狀和大小有怎樣的變化?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線y=kx+b與拋物線y=ax2(a>0)相交于A、B兩點(點A在點B的左側),與y軸正半軸相交于點C,過點A作AD⊥x軸,垂足為D.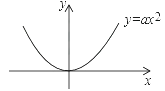
(1)若∠AOB=60°,AB∥x軸,AB=2,求a的值;
(2)若∠AOB=90°,點A的橫坐標為﹣4,AC=4BC,求點B的坐標;
(3)延長AD、BO相交于點E,求證:DE=CO.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在矩形ABCD中,AB<AD,對角線AC,BD相交于點O,動點P由點A出發,沿AB-BC→CD向點D運動設點P的運動路程為x,△AOP的面積為y,y與x的函數關系圖象如圖②所小示,則AD的長為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com