【題目】4836′的余角是_________，補角是_________.
課課練江蘇系列答案
名牌中學課時作業系列答案
明天教育課時特訓系列答案科目：初中數學 來源： 題型：
【題目】如圖，直線l1的解析表達式為：y=﹣3x+3，且l1與x軸交于點D，直線l2經過點A，B，直線l1 ， l2交于點C．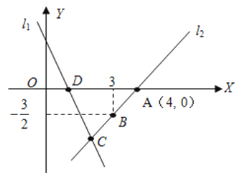
（1）求點D的坐標；
（2）求直線l2的解析表達式；
（3）求△ADC的面積；
（4）在直線l2上存在異于點C的另一點P，使得△ADP與△ADC的面積相等，請直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P( x, y1)與Q (x, y2)分別是兩個函數圖象C1與C2上的任一點. 當a ≤ x ≤ b時，有-1 ≤ y1 - y2 ≤ 1成立，則稱這兩個函數在a ≤ x ≤ b上是“相鄰函數”，否則稱它們在a ≤ x ≤ b上是“非相鄰函數”.
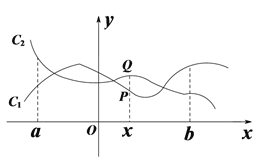
例如，點P(x, y1)與Q (x, y2)分別是兩個函數y = 3x+1與y = 2x - 1圖象上的任一點，當-3 ≤ x ≤ -1時，y1 - y2 = (3x + 1) - (2x - 1) = x + 2，通過構造函數y = x + 2并研究該函數在-3 ≤ x ≤ -1上的性質，得到該函數值的范圍是-1 ≤ y ≤ 1，所以-1 ≤ y1 - y2 ≤ 1成立，因此這兩個函數在-3 ≤ x ≤ -1上是“相鄰函數”.
（1）判斷函數y = 3x + 2與y = 2x + 1在－2 ≤ x≤ 0上是否為“相鄰函數”，說明理由；
（2）若函數y = x2 - x與y = x - a在0 ≤ x ≤ 2上是“相鄰函數”，求a的取值范圍；
（3）若函數y =
與y =－2x + 4在1 ≤ x ≤ 2上是“相鄰函數”，直接寫出a的最大值與最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是二次函數y=ax2+bx+c圖象的一部分，其對稱軸為x=﹣1，且過點（﹣3，0）．下列說法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（
，y2）是拋物線上兩點，則y1＞y2．
其中說法正確的是（ ）
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
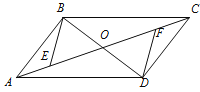
【題目】如圖，□ABCD的對角線AC、BD相交于點O，AE＝CF．
（1）求證：△BOE≌△DOF；
（2）若BD＝EF，連接DE、BF，判斷四邊形EBFD的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，AB=4，AD=3，以頂點D為圓心作半徑為r的圓，若點A，B，C中至少有一個點在圓內，且至少有一個點在圓外，則r的值可以是下列選項中的（ ）
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
