
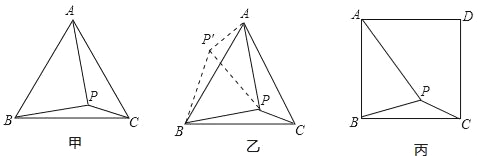
【題目】如圖甲,在等邊三角形ABC內有一點P,且PA=2,PB=![]() ,PC=1,求∠BPC度數的大小和等邊三角形ABC的邊長.
,PC=1,求∠BPC度數的大小和等邊三角形ABC的邊長.
解題思路是:將△BPC繞點B逆時針旋轉60°,如圖乙所示,連接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的邊長為 .
如圖丙,在正方形ABCD內有一點P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度數的大小;
(4)求正方形ABCD的邊長.
【答案】(1)等邊 直角 150°;(2)![]() ;(3)135°;(4)
;(3)135°;(4)![]() .
.
【解析】
(1)將△BPC繞點B順時針旋轉60°,畫出旋轉后的圖形(如圖2),連接PP′,可得△P′PB是等邊三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可證),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,
(2)過點B作BM⊥AP′,交AP′的延長線于點M,進而求出等邊△ABC的邊長為![]() ,問題得到解決.
,問題得到解決.
(3)求出![]() ,根據勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
,根據勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
(4)過點B作BF⊥AE,交AE的延長線于點F,求出FE=BF=1,AF=2,關鍵勾股定理即可求出AB.
解:(1)∵△ABC是等邊三角形,
∴∠ABC=60°,
將△BPC繞點B順時針旋轉60°得出△ABP′,
∴![]()
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等邊三角形,
∴![]()
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,則△PP′A是 直角三角形;
∴∠BPC=∠AP′B=90°+60°=150°;
(2)過點B作BM⊥AP′,交AP′的延長線于點M,
∴![]()
由勾股定理得: ![]()
∴![]()
由勾股定理得: ![]()
故答案為:(1)等邊;直角;150;![]() ;
;
(3)將△BPC繞點B逆時針旋轉90°得到△AEB,
與(1)類似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴![]() ,
,
由勾股定理得:EP=2,
∵![]()
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°;
(4)過點B作BF⊥AE,交AE的延長線于點F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形邊長為![]() .
.
答:(3)∠BPC的度數是135°;
(4)正方形ABCD的邊長是![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:
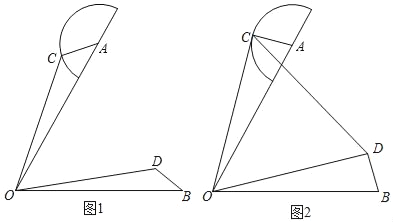
【題目】已知OA=OB=4,∠AOB=60°,半⊙A的半徑為1,點C是半圓上任意一點,連結OC,把OC繞點O順時針旋轉6
0°到OD的位置,連結BD.
(1)如圖1,求證:AC=BD.
(2)如圖2,當OC與半圓相切于點C時,求CD的長.
(3)直接寫出△AOC面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=90°,AB=12,BC=24,動點P從點A開始沿邊AB向終點B以每秒2個單位長度的速度移動,動點Q從點B開始沿邊BC以每秒4個單位長度的速度向終點C移動,如果點P、Q分別從點A、B同時出發,那么△PBQ的面積S隨出發時間t(s)如何變化?寫出函數關系式及t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,四邊形ABCD是正方形,點E是邊BC上一點,點F在射線CM上,∠AEF=90°,AE=EF,過點F作射線BC的垂線,垂足為H,連接AC.
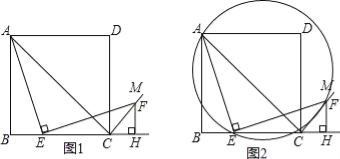
(1)試判斷BE與FH的數量關系,并說明理由;
(2)求證:∠ACF=90°;
(3)連接AF,過A、E、F三點作圓,如圖2,若EC=4,∠CEF=15°,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
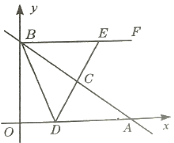
【題目】如圖,在平面直角坐標系中,直線![]() 分別交
分別交![]() 軸于
軸于![]() 兩點,
兩點,![]() 為線段
為線段![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一動點(不與
上一動點(不與![]() 點重合),射線
點重合),射線![]() 軸,延長
軸,延長![]() 交
交![]() 于點
于點![]() .
.
(1)求證:![]() ;
;
(2)連接![]() ,記
,記![]() 的面積為
的面積為![]() ,求
,求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)是否存在![]() 的值,使得
的值,使得![]() 是以
是以![]() 為腰的等腰三角形?若存在,求出所有符合條件的
為腰的等腰三角形?若存在,求出所有符合條件的![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=﹣x+3與拋物線![]() 交于A、B兩點,點A在x軸上,點B的橫坐標為
交于A、B兩點,點A在x軸上,點B的橫坐標為![]() .動點P在拋物線上運動(不與點A、B重合),過點P作y軸的平行線,交直線AB于點Q.當PQ不與y軸重合時,以PQ為邊作正方形PQMN,使MN與y軸在PQ的同側,連結PM.設點P的橫坐標為m.
.動點P在拋物線上運動(不與點A、B重合),過點P作y軸的平行線,交直線AB于點Q.當PQ不與y軸重合時,以PQ為邊作正方形PQMN,使MN與y軸在PQ的同側,連結PM.設點P的橫坐標為m.
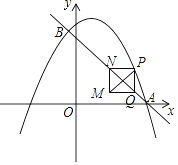
(1)求b、c的值.
(2)當點N落在直線AB上時,直接寫出m的取值范圍.
(3)當點P在A、B兩點之間的拋物線上運動時,設正方形PQMN的周長為C,求C與m之間的函數關系式,并寫出C隨m增大而增大時m的取值范圍.
(4)當△PQM與坐標軸有2個公共點時,直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A、B的坐標分別為(﹣3,0)、(3,0),點P在反比例函數y= ![]() 的圖象上.若△PAB為直角三角形,則滿足條件的點P的個數為( )
的圖象上.若△PAB為直角三角形,則滿足條件的點P的個數為( )
A. 2個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車廠決定把一塊長100m、寬60m的矩形空地建成停車場.設計方案如圖所示,陰影區域為綠化區(四塊綠化區為全等的矩形),空白區域為停車位,且四周的4個出口寬度相同,其寬度不小于28m,不大于52m.設綠化區較長邊為xm,停車場的面積為ym2
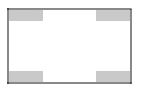
(1)直接寫出:
①用x的式子表示出口的寬度為_____.
②y與x的函數關系式及x的取值范圍.
(2)求停車場的面積y的最大值.
(3)預計停車場造價為100元/m2,綠化區造價為50元/m2.如果汽車廠投資不得超過540000元建造,當x為整數時,共有幾種建造方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
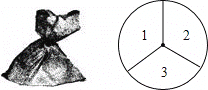
【題目】一個不透明的袋子中裝有4個完全相同的小球,分別標有數字1、2、3、4,另有一個可以自由轉動的轉盤.被分成面積相等的3個扇形區,分別標有數字1、2、3(如圖所示).小亮和小麗想通過游戲來決定誰代表學校參加歌詠比賽.游戲規則為:一人從袋子中摸出一個小球,另一個人轉動轉盤,如果從袋中所摸球上的數字與轉盤上轉出數字之和小于4,那么小麗去,否則小亮去.
(1)請用適當的方法求小麗參加比賽的概率;
(2)你認為該游戲公平嗎?請說明理由;若不公平,請修改該游戲規則,使游戲公平.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com