
【題目】(1)如圖,在△ABC中,∠A=42°,∠ABC和∠ACB的平分線相交于點D,求∠BDC的度數.
(2)在(1)中去掉∠A=42°這個條件,請探究∠BDC和∠A之間的數量關系.

【答案】(1)111° (2)90°+![]() ∠A
∠A
【解析】試題分析:(1)由∠A的度數,根據三角形的內角和定理,求出∠ABC、∠ACB度數,再求出∠DBC與∠DCB的度數和,進而求出∠BDC的度數.
(2)∠BDC+∠DBC+∠DCB=180°,∠A+∠ABC+∠ACB=180°,又有∠ABC+∠ACB=2(∠DBC+∠DCB),可得∠BDC和∠A之間的數量關系.
試題解析:
(1)∵∠ABC+∠ACB =180°-∠A=180°-42°=138°,
又∵BD,CD分別是∠ABC,∠ACB的平分線,
∴∠CBD=![]() ∠ABC,∠BCD=
∠ABC,∠BCD=![]() ∠ACB,
∠ACB,
∴∠CBD+∠BCD=![]() (∠ABC+∠ACB)=69°,
(∠ABC+∠ACB)=69°,
∴∠BDC =180°-(∠CBD+∠BCD)=180°-69°=111°.
(2)90°+![]() ∠A.理由如下:
∠A.理由如下:
∵∠ABC+∠ACB =180°-∠A,
又∵BD,CD分別是∠ABC,∠ACB的平分線,
∴∠CBD=![]() ∠ABC,∠BCD=
∠ABC,∠BCD=![]() ∠ACB,
∠ACB,
∴∠CBD+∠BCD=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BDC =180°-(90°-![]() ∠A)=180°-90°+
∠A)=180°-90°+![]() ∠A=90°+
∠A=90°+![]() ∠A.
∠A.


 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD,AB=AC,點E,F分別是BC,AD的中點,連接AE,CF.
(1)求證:四邊形AECF是矩形;
(2)若AB=8,求菱形的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明爸爸經營的水果店出售一種優質熱帶水果,正在上初三的小明經過調查和計算,發現這種水果每月的銷售量y(千克)與銷售單價x(元)之間存在著一次函數關系:y=-10x+500(20≤x≤50).下面是他們的一次對話:
小明:“您要是告訴我咱家這種水果的進價是多少?我就能幫你預測好多信息呢!”
爸爸:“咱家這種水果的進價是每千克20元”
聰明的你,也來解答一下小明想要解決的兩個問題:
(1)若每月獲得利潤w(元)是銷售單價x(元)的函數,求這個函數的表達式.
(2)當銷售單價為多少元時,每月可獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AC是ABCD的一條對角線,過AC中點O的直線分別交AD,BC于點E,F.
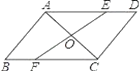
(1)求證:AE=CF;
(2)連接AF,CE.
①當EF和AC滿足條件 時,四邊形AFCE是菱形;
②若AB=1,BC=2,∠B=60°,則四邊形AFCE為矩形時,EF的長是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九(1)班組織班級聯歡會,最后進入抽獎環節,每名同學都有一次抽獎機會,抽獎方案如下:將一副撲克牌中點數為“2”,“3”,“3”,“5”,“6”的五張牌背面朝上洗勻,先從中抽出1張牌,再從余下的4張牌中抽出1張牌,記錄兩張牌點數后放回,完成一次抽獎,記每次抽出兩張牌點數之差為![]() ,按表格要求確定獎項.
,按表格要求確定獎項.

(1)用列表或畫樹狀圖的方法求出甲同學獲得一等獎的概率;
(2)是否每次抽獎都會獲獎,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只不透明的袋子中裝有3個球,球上分別標有數字0,1,2,這些球除了數字外其余都相同,甲、以兩人玩摸球游戲,規則如下:先由甲隨機摸出一個球(不放回),再由乙隨機摸出一個球,兩人摸出的球所標的數字之和為偶數時則甲勝,和為奇數時則乙勝.
(1)用畫樹狀圖或列表的方法列出所有可能的結果;
(2)這樣的游戲規則是否公平?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC的內切圓⊙O與AB、BC、CA分別相切于點D、E、F,且∠ACB=90°,AB=5,BC=3,點P在射線AC上運動,過點P作PH⊥AB,垂足為H.
(1)直接寫出線段AD及⊙O半徑的長;
(2)設PH=x,PC=y,求y關于x的函數關系式;
(3)當PH與⊙O相切時,求相應的y值.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com