
【題目】如圖,直線![]() 、
、![]() 相交于點
相交于點![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]()
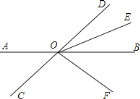
![]() 求
求![]() 的度數;
的度數;
![]() 求
求![]() 的度數.
的度數.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根據鄰補角的和等于180°求出∠BOD的度數,然后根據角平分線的定義解答;
(2)先求出∠COE的度數,再根據角平分線的定義求出∠COF,然后根據對頂角相等求出∠AOC,再根據∠AOF=∠AOC+∠COF,代入數據進行計算即可得解.
(1)∵∠AOD:∠BOD=2:1,∠AOD+∠BOD=180°,∴∠BOD=![]() ×180°=60°.
×180°=60°.
∵OE平分∠BOD,∴∠DOE=![]() ∠BOD=
∠BOD=![]() ×60°=30°;
×60°=30°;
(2)∠COE=∠COD﹣∠DOE=180°﹣30°=150°.
∵OF平分∠COE,∴∠COF=![]() ∠COE=
∠COE=![]() ×150°=75°.
×150°=75°.
∵∠AOC=∠BOD=60°(對頂角相等),∴∠AOF=∠AOC+∠COF=60°+75°=135°.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設立了可以自由轉動的轉盤(如圖,轉盤被均勻分為20份),并規定:顧客每購買200元的商品,就能獲得一次轉動轉盤的機會.如果轉盤停止后,指針正好對準紅色、黃色、綠色區域,那么顧客就可以分別獲得200元、100元、50元的購物券,憑購物券可以在該商場繼續購物.如果顧客不愿意轉轉盤,那么可以直接獲得購物券30元.
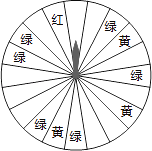
(1)求轉動一次轉盤獲得購物券的概率;
(2)轉轉盤和直接獲得購物券,你認為哪種方式對顧客更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,AD是△ABC的角平分線,點O為AB的中點,連接DO并延長到點E,使OE=OD,連接AE,BE.

(1)求證:四邊形AEBD是矩形;
(2)當△ABC滿足什么條件時,矩形AEBD是正方形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
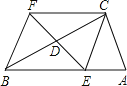
【題目】如圖,在△ABC中,∠ACB=90°,且DE是△ABC的中位線.延長ED到F,使DF=ED,連接FC,FB.回答下列問題:
(1)試說明四邊形BECF是菱形.
(2)當![]() 的大小滿足什么條件時,菱形BECF是正方形?請回答并證明你的結論.
的大小滿足什么條件時,菱形BECF是正方形?請回答并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一袋中裝有形狀大小都相同的四個小球,每個小球上各標有一個數字,分別是1,3,4,7.現規定從袋中任取一個小球,對應的數字作為一個兩位數的個位數;然后將小球放回袋中并攪拌均勻,再任取一個小球,對應的數字作為這個兩位數的十位數.
(1)寫出按上述規定得到所有可能的兩位數;
(2)從這些兩位數中任取一個,求其算術平方根大于5且小于8的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c與x軸交于A(1,0),B(3,0)兩點,與y軸交于點C(0,3).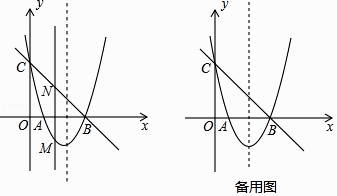
(1)求拋物線的解析式;
(2)若點M是x軸下方的拋物線上的一個動點,過點M作MN⊥x軸,交直線BC于點N,求四邊形MBNA的最大面積,并求出點M的坐標;
(3)在拋物線上是否存在一點P,使△BCP為直角三角形?若存在,求出P點坐標,如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖![]() ,點
,點![]() 是線段
是線段![]() 上一定點,
上一定點,![]() ,
,![]() 、
、![]() 兩點分別從
兩點分別從![]() 、
、![]() 出發以
出發以![]() 、
、![]() 的速度沿直線
的速度沿直線![]() 向左運動,運動方向如箭頭所示(
向左運動,運動方向如箭頭所示(![]() 在線段
在線段![]() 上,
上,![]() 在線段
在線段![]() 上)
上)
![]() 若
若![]() ,當點
,當點![]() 、
、![]() 運動了
運動了![]() ,此時
,此時![]() ________,
________,![]() ________;(直接填空)
________;(直接填空)
![]() 當點
當點![]() 、
、![]() 運動了
運動了![]() ,求
,求![]() 的值.
的值.
![]() 若點
若點![]() 、
、![]() 運動時,總有
運動時,總有![]() ,則
,則![]() ________(填空)
________(填空)
![]() 在
在![]() 的條件下,
的條件下,![]() 是直線
是直線![]() 上一點,且
上一點,且![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了更好的保護美麗圖畫的邛海濕地,西昌市污水處理廠決定先購買A、B兩型污水處理設備共20臺,對邛海濕地周邊污水進行處理,每臺A型污水處理設備12萬元,每臺B型污水處理設備10萬元.已知1臺A型污水處理設備和2臺B型污水處理設備每周可以處理污水640噸,2臺A型污水處理設備和3臺B型污水處理設備每周可以處理污水1080噸.
(1)求A、B兩型污水處理設備每周分別可以處理污水多少噸?
(2)經預算,市污水處理廠購買設備的資金不超過230萬元,每周處理污水的量不低于4500噸,請你列舉出所有購買方案,并指出哪種方案所需資金最少?最少是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AB的中點,點D在線段CB上.
![]()
(1)圖中共有 條線段.
(2)圖中AD=AC+CD,BC=AB﹣AC,類似地,請你再寫出兩個有關線段的和與差的關系式:
① ;② .
(3)若AB=8,DB=1.5,求線段CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com