【題目】在平面直角坐標系
中，直線
與雙曲線
相交于點
.
（1）求反比例函數的表達式：
（2）畫出直線和雙曲線的示意圖；
（3）直接寫出
的解集______；
（4）若點
是坐標軸負半軸上一點，且滿足
.直接寫出點的坐標______.
科目：初中數學 來源： 題型：
【題目】某公司經銷一種成本為10元的產品，經市場調查發現，在一段時間內，銷售量
（件）與銷售單價
（ 元/件 ）的關系如下表：
|
| 15 | 20 | 25 | 30 |
|
|
| 550 | 500 | 450 | 400 |
|
設這種產品在這段時間內的銷售利潤為
（元），解答下列問題：
（1）如是的一次函數，求與的函數關系式；
（2）求銷售利潤與銷售單價之間的函數關系式；
（3）求當為何值時，的值最大？最大是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
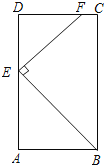
【題目】如圖，在矩形ABCD中，AB=6，AD=12，點E在AD邊上，且AE=8，EF⊥BE交CD于F．
（1）求證：△ABE∽△DEF；
（2）求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在開展“學雷鋒社會實踐”活動中，某校為了解全校1200名學生參加活動的情況，隨機調查了50名學生每人參加活動的次數，并根據數據繪成條形統計圖如下：
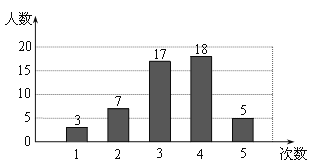
（Ⅰ）求這50個樣本數據的平均數、眾數和中位數；
（Ⅱ）根據樣本數據，估算該校1200名學生共參加了多少次活動．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
（1）若
求該拋物線與x軸的交點坐標；
（2）若
，是否存在實數
,使得相應的y=1，若有，請指明有幾個并證明你的結論，若沒有，闡述理由。
（3）若
且拋物線在
區間上的最小值是-3，求b的值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中，給出如下定義：若點
在圖形
上，點
在圖形
上，如果
兩點間的距離有最小值，那么稱這個最小值為圖形
的“近距離”，記為
.特別地，當圖形與圖形有公共點時，
.
已知
，
，
，
（1）
點
，點
，點，線段
；
（2）⊙
半徑為
，
①當
時，求⊙與線段
的“近距離”⊙，線段
；
②若⊙，
，則
.
（3）
為
軸上一點，⊙的半徑為1，點
關于軸的對稱點為點
，⊙與
的“近距離”⊙，
，請直接寫出圓心的橫坐標
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
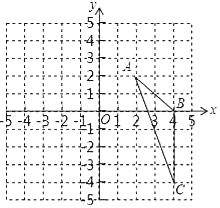
【題目】如圖，在平面直角坐標系中，已知△ABC三個頂點的坐標分別是A（2，2），B（4，0），C（4，﹣4）．
（1）請在圖中，畫出△ABC向左平移6個單位長度后得到的△A1B1C1；
（2）以點O為位似中心，將△ABC縮小為原來的
，得到△A2B2C2，請在圖中y軸右側，畫出△A2B2C2，并求出∠A2C2B2的正弦值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們定義一種新函數：形如
的函數叫做“鵲橋”函數．小麗同學畫出了“鵲橋”函數
的圖象(如圖所示)，并寫出下列五個結論：①圖象與坐標軸的交點為
，
和
；②圖象具有對稱性，對稱軸是直線
；③當
或
時，函數值
隨
值的增大而增大；④當
或
時，函數的最小值是
；⑤當時，函數的最大值是
，其中正確結論的個數是( )
A.B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，⊙O過ABCD的三頂點A、D、C，邊AB與⊙O相切于點A，邊BC與⊙O相交于點H，射線AD交邊CD于點E，交⊙O于點F，點P在射線AO上，且∠PCD=2∠DAF．
（1）求證：△ABH是等腰三角形；
（2）求證：直線PC是⊙O的切線；
（3）若AB=2，AD=
，求⊙O的半徑．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
