
【題目】如圖,ABCD紙片,∠A=120°,AB=4,BC=5,剪掉兩個角后,得到六邊形AEFCGH,它的每個內角都是120°,且EF=1,HG=2,則這個六邊形的周長為( ) 
A.12
B.15
C.16
D.18
科目:初中數學 來源: 題型:
【題目】△ABC的三邊長分別為a,b,c,下列條件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③a2=(b+c)(b-c);④a:b:c=5:12:13,其中能判斷△ABC是直角三角形的個數有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校準備組織部分學生到少年宮參加活動,陳老師從少年宮帶回來兩條信息:
信息一:按原來報名參加的人數,共需要交費用320元,如果參加的人數能夠增加到原來人數的2倍,就可以享受優惠,此時只需交費用480元;
信息二:如果能享受優惠,那么參加活動的每位同學平均分攤的費用比原來少4元.
根據以上信息,原來報名參加的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C、G是⊙O上兩點,且AC=CG,過點C的直線CD⊥BG于點D,交BA的延長線于點E,連接BC,交OD于點F.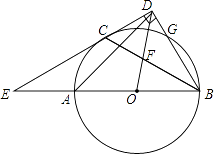
(1)求證:CD是⊙O的切線.
(2)若 ![]() ,求∠E的度數.
,求∠E的度數.
(3)連接AD,在(2)的條件下,若CD= ![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,∠CAB=30°,AC=8,半徑為2的⊙O從點A開始(如圖1)沿直線AB向右滾動,滾動時始終與直線AB相切(切點為D),當⊙O與△ABC只有一個公共點時滾動停止,作OG⊥AC于點G. 
(1)圖1中,⊙O在AC邊上截得的弦長AE=;
(2)當圓心落在AC上時,如圖2,判斷BC與⊙O的位置關系,并說明理由. 
(3)在⊙O滾動過程中,線段OG的長度隨之變化,設AD=x,OG=y,求出y與x的函數關系式,并直接寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
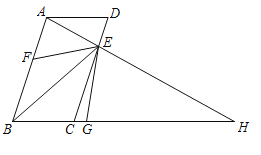
【題目】如圖,![]() ,點E是邊DC上一點,連接AE交BC的延長線于點H,點F是邊AB上一點,使得
,點E是邊DC上一點,連接AE交BC的延長線于點H,點F是邊AB上一點,使得![]() ,作
,作![]() 的角平分線
的角平分線![]() 交BH于點G,若
交BH于點G,若![]() ,則
,則![]() 的度數是( )
的度數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,EF∥AD,M,N是線段EF的六等分點,若把該正方形紙片卷成一個圓柱,使點A與點D重合,此時,底面圓的直徑為10cm,則圓柱上M,N兩點間的距離是cm.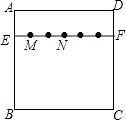
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com