
【題目】如圖,在正方形![]() 中,點
中,點![]() 、
、![]() 是正方形內兩點,
是正方形內兩點,![]() ,
,![]() ,為探索這個圖形的特殊性質,某數學興趣小組經歷了如下過程:
,為探索這個圖形的特殊性質,某數學興趣小組經歷了如下過程:

(1)在圖1中,連接![]() ,且
,且![]()
①求證:![]() 與
與![]() 互相平分;
互相平分;
②求證:![]() ;
;
(2)在圖2中,當![]() ,其它條件不變時,
,其它條件不變時,![]() 是否成立?若成立,請證明:若不成立,請說明理由.
是否成立?若成立,請證明:若不成立,請說明理由.

(3)在圖3中,當![]() ,
,![]() ,
,![]() 時,求
時,求![]() 之長.
之長.

【答案】(1)①詳見解析;②詳見解析;(2)當BE≠DF時,(BE+DF)2+EF2=2AB2仍然成立,理由詳見解析;(3)![]()
【解析】
(1)①連接ED、BF,證明四邊形BEDF是平行四邊形,根據平行四邊形的性質證明;②根據正方形的性質、勾股定理證明;
(2)過D作DM⊥BE交BE的延長線于M,連接BD,證明四邊形EFDM是矩形,得到EM=DF,DM=EF,∠BMD=90°,根據勾股定理計算;
(3)過P作PE⊥PD,過B作BELPE于E,根據(2)的結論求出PE,結合圖形解答.

(1)證明:①連接ED、BF,
∵BE∥DF,BE=DF,
∴四邊形BEDF是平行四邊形,
∴BD、EF互相平分;
②設BD交EF于點O,則OB=OD=![]() BD,OE=OF=
BD,OE=OF=![]() EF.
EF.
∵EF⊥BE,
∴∠BEF=90°.
在Rt△BEO中,BE2+OE2=OB2.
∴(BE+DF)2+EF2=(2BE)2+(2OE)2=4(BE2+OE2)=4OB2=(2OB)2=BD2.
在正方形ABCD中,AB=AD,BD2=AB2+AD2=2AB2.
∴(BE+DF)2+EF2=2AB2;
(2)解:當BE≠DF時,(BE+DF)2+EF2=2AB2仍然成立,

理由如下:如圖2,過D作DM⊥BE交BE的延長線于M,連接BD.
∵BE∥DF,EF⊥BE,
∴EF⊥DF,
∴四邊形EFDM是矩形,
∴EM=DF,DM=EF,∠BMD=90°,
在Rt△BDM中,BM2+DM2=BD2,
∴(BE+EM)2+DM2=BD2.
即(BE+DF)2+EF2=2AB2;
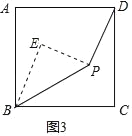
(3)解:過P作PE⊥PD,過B作BE⊥PE于E,
則由上述結論知,(BE+PD)2+PE2=2AB2.
∵∠DPB=135°,
∴∠BPE=45°,
∴∠PBE=45°,
∴BE=PE.
∴△PBE是等腰直角三角形,
∴BP=![]() BE,
BE,
∵![]() BP+2PD=4
BP+2PD=4![]() ,
,
∴2BE+2PD=4![]() ,即BE+PD=2
,即BE+PD=2![]() ,
,
∵AB=4,
∴(2![]() )2+PE2=2×42,
)2+PE2=2×42,
解得,PE=2![]() ,
,
∴BE=2![]() ,
,
∴PD=2![]() ﹣2
﹣2![]() .
.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:初中數學 來源: 題型:
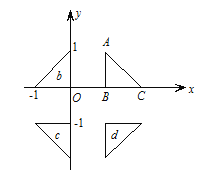
【題目】如圖,等腰直角三角形![]() 分別沿著某條直線對稱得到圖形
分別沿著某條直線對稱得到圖形![]() .若上述對稱關系保持不變,平移
.若上述對稱關系保持不變,平移![]() ,使得四個圖形能夠圍成一個不重疊且無縫隙的正方形,此時點
,使得四個圖形能夠圍成一個不重疊且無縫隙的正方形,此時點![]() 的坐標和正方形的邊長為( )
的坐標和正方形的邊長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
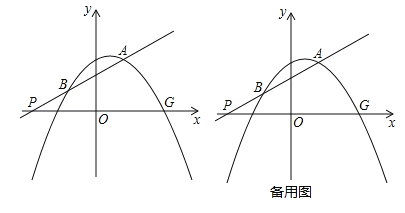
【題目】如圖,二次函數y=﹣![]() x2+mx+n的圖象經過點A(2,3),與x軸的正半軸交于點G(1+
x2+mx+n的圖象經過點A(2,3),與x軸的正半軸交于點G(1+![]() ,0);一次函數y=kx+b的圖象經過點A,且交x軸于點P,交拋物線于另一點B,又知點A,B位于點P的同側.
,0);一次函數y=kx+b的圖象經過點A,且交x軸于點P,交拋物線于另一點B,又知點A,B位于點P的同側.
(1)求這個二次函數的解析式;
(2)若PA=3PB,求一次函數的解析式;
(3)在(2)的條件下,當k>0時,拋物線的對稱軸上是否存在點C,使⊙C同時與x軸和直線AP都相切?如果存在,請求出點C的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,以下幾種說法中:①![]() 和
和![]() 是同位角;②
是同位角;②![]() 和
和![]() 是同位角;③
是同位角;③![]() 和
和![]() 是內錯角;④
是內錯角;④![]() 和
和![]() 是同旁內角;⑤
是同旁內角;⑤![]() 和
和![]() 是同位角;⑥
是同位角;⑥![]() 和
和![]() 是同位角;正確的個數是( )
是同位角;正確的個數是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
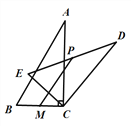
【題目】如圖,在![]() 中,
中,![]() ,將
,將![]() 繞頂點
繞頂點![]() 逆時針旋轉得到Rt△DEC,點M是BC的中點,點P是DE的中點,連接PM,若BC =2,∠BAC=30°,則線段PM的最大值是 ( )
逆時針旋轉得到Rt△DEC,點M是BC的中點,點P是DE的中點,連接PM,若BC =2,∠BAC=30°,則線段PM的最大值是 ( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD向右平移一段距離后得到四邊形![]() .
.

(1)找出圖中存在的平行且相等的四條線段(即四條線段全部互相平行且相等);
(2)找出圖中存在的四組相等的角;
(3)四邊形ABCD與四邊形![]() 的形狀、大小相同嗎?為什么?
的形狀、大小相同嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=k1x+b的圖象分別與x軸、y軸的正半軸交于 A,B 兩點,且與反比例函數y=![]() 交于 C,E 兩點,點 C 在第二象限,過點 C 作CD⊥x軸于點 D,AC=2
交于 C,E 兩點,點 C 在第二象限,過點 C 作CD⊥x軸于點 D,AC=2![]() ,OA=OB=1.
,OA=OB=1.

(1)△ADC 的面積;
(2)求反比例函數y= ![]() 與一次函數的y=k1x+b表達式.
與一次函數的y=k1x+b表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知M=(a+24)x3﹣10x2+10x+5是關于x的二次多項式,且二次項系數和一次項系數分別為b和c,在數軸上A、B、C三點所對應的數分別是a、b、c.
![]()
(1)則a= ,b= ,c= .
(2)有一動點P從點A出發,以每秒4個單位的速度向右運動,多少秒后,P到A、B、C的距離和為40個單位?
(3)在(2)的條件下,當點P移動到點B時立即掉頭,速度不變,同時點T和點Q分別從點A和點C出發,向左運動,點T的速度1個單位/秒,點Q的速度5個單位/秒,設點P、Q、T所對應的數分別是xP、xQ、xT,點Q出發的時間為t,當![]() <t<
<t<![]() 時,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
時,求2|xP﹣xT|+|xT﹣xQ|+2|xQ﹣xP|的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)把數軸補充完整.
(2)在數軸上表示下列各數:3![]() ,﹣4,﹣(﹣1.5),﹣|﹣2|.
,﹣4,﹣(﹣1.5),﹣|﹣2|.
(3)用“<”連接起來._____________
(4)﹣|﹣2|與﹣4之間的距離是_________.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com