
【題目】如圖,在等腰直角△ABC中, ![]() 點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且
點D是斜邊BC的中點,點E、F分別為AB、AC邊上的點,且![]() .
.
(1)判斷![]() 與
與![]() 的大小關系,并說明理由;
的大小關系,并說明理由;
(2)若BE=12,CF=5,求△![]() 的面積.
的面積.

【答案】(1)DF=DE;(2)△DEF的面積是![]()
【解析】試題分析:(1)連接AD,首先利用等腰三角形的性質得到AD⊥BC,AD=CD=BD,從而得到∠CDF=∠ADE,然后利用ASA證得DCF≌△ADE后即可證得DF=DE;
(2)由(1)知:AE=CF,AF=BC,DE=DF,即△EDF為等腰直角三角形,在Rt△AEF中,運用勾股定理可將EF的值求出,進而可求出DE、DF的值,代入S△EDF=![]() DE2進行求解.
DE2進行求解.
試題解析:(1)DF=DE,理由如下:
如圖,連接AD,
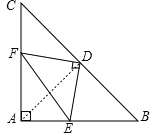
∵AB=AC,D為BC的中點,
∴AD⊥BC,AD=CD=BD,
∵DE⊥DF,
∴∠CDF+∠ADF=∠EDA+∠ADF,
即∠CDF=∠ADE,
在△DCF和△DAE中,
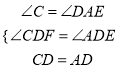 ,
,
∴△DCF≌△DAE(ASA),
∴DF=DE;
(2)由(1)知:AE=CF=5,同理AF=BE=12.
∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169.
∴EF=13,
又∵由(1)知:△AED≌△CFD,
∴DE=DF,
∴△DEF為等腰直角三角形,DE2+DF2=EF2=169,
∴DE=DF=![]() ,
,
∴S△DEF=![]() ×(
×(![]() )2=
)2=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】2019年江蘇省糧食總產達40 540 000噸,居全國第四位.用科學記數法表示40 540 000是( )
A.4054×104B.4.054×104C.4.054×107D.4054×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y1=x2+bx+c的頂點坐標為(﹣1,1),直線1的解析式為y2=2mx+3m2+4nm+4n2,且l與x軸、y軸分別交于A、B兩點.
(1)求b、c的值;
(2)若函數y1+y2的圖象與x軸始終有公共點,求直線l的解析式;
(3)點P是拋物線對稱軸上的一個動點,是否存在點P,使△PAB為等腰角形?若存在,直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畢達哥拉斯學派對“數”與“形”的巧妙結合作了如下研究: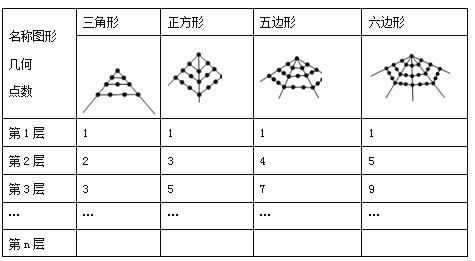
(1)六邊形第5層的幾何點數是 ;第n層的幾何點數是 .
(2)在第 層時,六邊形的幾何點數是三角形的幾何點數的3.5倍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市2017年實現生產總值達280億的目標,用科學記數法表示“280億”為( )
A. 28×109 B. 2.8×108 C. 2.8×109 D. 2.8×1010
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com