
【題目】對每個數位數字均不為零且互不相等的一個三位正整數![]() ,若將
,若將![]() 的十位數字與百位數字交換位置,得到一個新的三位數
的十位數字與百位數字交換位置,得到一個新的三位數![]() ,我們稱
,我們稱![]() 為
為![]() 的“置換數”,如:
的“置換數”,如:![]() 的“置效為“
的“置效為“![]() ”;若由
”;若由![]() 的百位、十位、個位上的數字任選兩個組成一個新的兩位數,所有新的兩位數之和記為
的百位、十位、個位上的數字任選兩個組成一個新的兩位數,所有新的兩位數之和記為![]() ,我們稱
,我們稱![]() 為
為![]() 的“行生數”.如
的“行生數”.如![]() :因為
:因為![]() 所以
所以![]() 的“衍生數”為
的“衍生數”為![]() .
.
(1)直接寫出![]() 的“置換數”,并求
的“置換數”,并求![]() 的“衍生數”;
的“衍生數”;
(2)對每個數位數字均不為零且互不相等的一個三位正整數![]() ,設十位數字為
,設十位數字為![]() ,若
,若![]() 的“衍生數”與
的“衍生數”與![]() 的“置換數”之差為
的“置換數”之差為![]() ,求
,求![]() .
.
【答案】(1)897;528;(2)814
【解析】
(1)直接根據“置換數”和“衍生數”的定義解答即可;
(2)設x的百位數字為a,各位數字為b,根據![]() 的“衍生數”與
的“衍生數”與![]() 的“置換數”之差為
的“置換數”之差為![]() 列出關于a和b的二元一次方程,結合a和b是互不相等的正整數求解即可.
列出關于a和b的二元一次方程,結合a和b是互不相等的正整數求解即可.
(1)![]() 的“置換數”是:897,
的“置換數”是:897, ![]() 的“衍生數”是:98+97+89+87+78+79=528;
的“衍生數”是:98+97+89+87+78+79=528;
(2)設x的百位數字為a,各位數字為b,則 的“衍生數”是10+a+10+b+10a+1+10a+b+10b+1+10b+a=22a+22b+22;x 的“置換數”是100+10a+b,由題意得,
22a+22b+22-100-10a-b=102,
即4a+7b=60,
∵a和b是互不相等的正整數,
∴a=8,b=4,
∴x=814.


 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
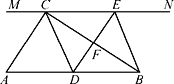
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上一點,過點D作DE⊥BC,交直線MN于E,垂足為F,連接CD,BE.
(1)求證:CE=AD;
(2)當D為AB中點時,四邊形BECD是什么特殊四邊形?說明你的理由;
(3)若D為AB中點,則當∠A的大小滿足什么條件時,四邊形BECD是正方形?請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下列材料,然后解答問題:
材料1:從三張不同的卡片中選出兩張排成一列,有6種不同的排法,抽象成數學問題就是從3個不同的元素中選取2個元素的排列,排列數記為A32=3×2=6.
一般地,從n個不同的元素中選取m個元素的排列數記作Anm.
Anm=n(n﹣1)(n﹣2)(n﹣3)…(n﹣m+1)(m≤n)
例:從5個不同的元素中選取3個元素排成一列的排列數為:A53=5×4×3=60.
材料2:從三張不同的卡片中選取兩張,有3種不同的選法,抽象成數學問題就是從3個元素中選取2個元素的組合,組合數為![]() .
.
一般地,從n個不同的元素中取出m個元素的組合數記作Cnm,
Cnm=![]() (m≤n)
(m≤n)
例:從6個不同的元素選3個元素的組合數為:![]() .
.
問:(1)從某個學習小組8人中選取3人參加活動,有 種不同的選法;
(2)從7個人中選取4人,排成一列,有 種不同的排法.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A(0,4)是直角坐標系y軸上一點,動點P從原點O出發,沿x軸正半軸運動,速度為每秒1個單位長度,以P為直角頂點在第一象限內作等腰Rt△APB.設P點的運動時間為t秒.
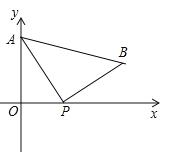
(1)若AB//x軸,求t的值;
(2)當t=3時,坐標平面內有一點M(不與A重合),使得以M、P、B為頂點的三角形和△ABP全等,請求出點M的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分線交于O點,過點O作BC的平行線交AB于M點,交AC于N點,則△AMN的周長為( )
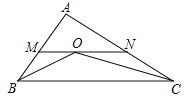
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市中小學全面開展“陽光體育”活動,某校在大課間中開設了A:體操,B:跑操,C:舞蹈,D:健美操四項活動,為了解學生最喜歡哪一項活動,隨機抽取了部分學生進行調查,并將調查結果繪制成了如下兩幅不完整的統計圖,請根據統計圖回答下列問題:
(1)這次被調查的學生共有 人.
(2)請將統計圖2補充完整.
(3)統計圖1中B項目對應的扇形的圓心角是 度.
(4)已知該校共有學生3600人,請根據調查結果估計該校喜歡健美操的學生人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國海軍亞丁灣護航十年,中國海軍被亞丁灣上來往的各國商船譽為“值得信賴的保護傘”如圖,在一次護航行動中,我國海軍監測到一批可疑快艇正快速向護航的船隊靠近.為保證船隊安全,我國海軍迅速派出甲、乙兩架直升機分別從相距20海里的船隊首(O點)尾(A點)前去攔截,4分鐘后同時到達B點將可疑快艇驅離.已知甲直升機每小時飛行180海里,航向為北偏東25°,乙直升機的航向為北偏西65°,求乙直升機的飛行速度.
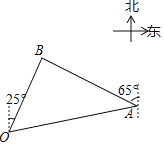
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在RI△ABC中,∠C=90°,AC=BC=4cm,點P從點A出發沿線段AB以![]() cm/s的速度向點B運動,設運動時間為ts.過點P作PD⊥AB,PD與△ABC的腰相交于點D.
cm/s的速度向點B運動,設運動時間為ts.過點P作PD⊥AB,PD與△ABC的腰相交于點D.
(1)當t=(4-2![]() )s時,求證:△BCD≌△BPD;
)s時,求證:△BCD≌△BPD;
(2)當t為何值時,S△APD=3S△BPD,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商城銷售A,B兩種自行車.A型自行車售價為2 100元/輛,B型自行車售價為1 750元/輛,每輛A型自行車的進價比每輛B型自行車的進價多400元,商城用80 000元購進A型自行車的數量與用64 000元購進B型自行車的數量相等.
(1)求每輛A,B兩種自行車的進價分別是多少?
(2)現在商城準備一次購進這兩種自行車共100輛,設購進A型自行車m輛,這100輛自行車的銷售總利潤為y元,要求購進B型自行車數量不超過A型自行車數量的2倍,總利潤不低于13 000元,求獲利最大的方案以及最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com