
某公司銷售一種進價為20元/個的計算機,其銷售量y(萬個)與銷售價格x(元/個)的變化如下表:
| 價格x(元/個) | … | 30 | 40 | 50 | 60 | … |
| 銷售量y(萬個) | … | 5 | 4 | 3 | 2 | … |
解:(1)根據表格中數據可得出:y與x是一次函數關系,設解析式為:y=ax+b,
則 ,解得:
,解得: 。
。
∴函數解析式為:y= x+8。
x+8。
(2)根據題意得:
z=(x﹣20)y﹣40=(x﹣20)( x+8)﹣40=
x+8)﹣40= x2+10x﹣200=
x2+10x﹣200= (x2﹣100x)﹣200
(x2﹣100x)﹣200
= [(x﹣50)2﹣2500]﹣200=
[(x﹣50)2﹣2500]﹣200= (x﹣50)2+50,
(x﹣50)2+50,
∵ <0,∴x=50,z最大=50。
<0,∴x=50,z最大=50。
∴該公司銷售這種計算器的凈得利潤z與銷售價格x)的函數解析式為z= x2+10x﹣200,銷售價格定為50元/個時凈得利潤最大,最大值是50萬元。
x2+10x﹣200,銷售價格定為50元/個時凈得利潤最大,最大值是50萬元。
(3)當公司要求凈得利潤為40萬元時,即 (x﹣50)2+50=40,解得:x1=40,x2=60。
(x﹣50)2+50=40,解得:x1=40,x2=60。
作函數圖象的草圖,
通過觀察函數y= (x﹣50)2+50的圖象,可知按照公司要求使凈得利潤不低于40萬元,則銷售價格的取值范圍為:40≤x≤60.
(x﹣50)2+50的圖象,可知按照公司要求使凈得利潤不低于40萬元,則銷售價格的取值范圍為:40≤x≤60.
而y與x的函數關系式為:y= x+8,y隨x的增大而減少,
x+8,y隨x的增大而減少,
∴若還需考慮銷售量盡可能大,銷售價格應定為40元/個。
解析試題分析:(1)根據數據得出y與x是一次函數關系,進而利用待定系數法求一次函數解析式。
(2)根據z=(x﹣20)y﹣40得出z與x的函數關系式,應用二次函數最值原理求解即可。
(3)首先求出40= (x﹣50)2+50時x的值,從而二次函數的性質根據得出x(元/個)的取值范圍,結合一次函數的性質即可求得結果。
(x﹣50)2+50時x的值,從而二次函數的性質根據得出x(元/個)的取值范圍,結合一次函數的性質即可求得結果。


科目:初中數學 來源: 題型:解答題
某公司營銷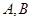 兩種產品,根據市場調研,發現如下信息:
兩種產品,根據市場調研,發現如下信息:
信息1:銷售 種產品所獲利潤
種產品所獲利潤 (萬元)與所售產品
(萬元)與所售產品 (噸)之間存在二次函數關系
(噸)之間存在二次函數關系 .當
.當 時,
時, ;當
;當 時,
時, .
.
信息2:銷售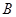 種產品所獲利潤
種產品所獲利潤 (萬元)與所售產品
(萬元)與所售產品 (噸)之間存在正比例函數關系
(噸)之間存在正比例函數關系 .
.
根據以上信息,解答下列問題:(1)求二次函數解析式;
(2)該公司準備購進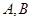 兩種產品共10噸,請設計一個營銷方案,使銷售
兩種產品共10噸,請設計一個營銷方案,使銷售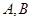 兩種產品獲得的利潤之和最大,最大利潤是多少?
兩種產品獲得的利潤之和最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在等邊△ABC中,AB=3,D、E分別是AB、AC上的點,且DE∥BC,將△ADE沿DE翻折,與梯形BCED重疊的部分記作圖形L.
(1)求△ABC的面積;
(2)設AD=x,圖形L的面積為y,求y關于x的函數解析式;
(3)已知圖形L的頂點均在⊙O上,當圖形L的面積最大時,求⊙O的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商家獨家銷售具有地方特色的某種商品,每件進價為40元.經過市場調查,一周的銷售量y件與銷售單價x(x≥50)元/件的關系如下表:
| 銷售單價x(元/件) | … | 55 | 60 | 70 | 75 | … |
| 一周的銷售量y(件) | … | 450 | 400 | 300 | 250 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
一汽車租賃公司擁有某種型號的汽車100輛.公司在經營中發現每輛車的月租金x(元)與每月租出的車輛數(y)有如下關系:
| x | 3000 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
| 租出的車輛數 | | 未租出的車輛數 | |
| 租出每輛車的月收益 | | 所有未租出的車輛每月的維護費 | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 與x軸相交于點A、B,與y軸相交于點C,拋物線的對稱軸與x軸相交于點M.P是拋物線在x軸上方的一個動點(點P、M、C不在同一條直線上).分別過點A、B作直線CP的垂線,垂足分別為D、E,連接點MD、ME.
與x軸相交于點A、B,與y軸相交于點C,拋物線的對稱軸與x軸相交于點M.P是拋物線在x軸上方的一個動點(點P、M、C不在同一條直線上).分別過點A、B作直線CP的垂線,垂足分別為D、E,連接點MD、ME.
(1)求點A,B的坐標(直接寫出結果),并證明△MDE是等腰三角形;
(2)△MDE能否為等腰直角三角形?若能,求此時點P的坐標;若不能,說明理由;
(3)若將“P是拋物線在x軸上方的一個動點(點P、M、C不在同一條直線上)”改為“P是拋物線在x軸下方的一個動點”,其他條件不變,△MDE能否為等腰直角三角形?若能,求此時點P的坐標(直接寫出結果);若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在平面直角坐標系中,一個二次函數的圖象經過點A(1,0)、B(3,0)兩點.
(1)寫出這個二次函數的對稱軸;
(2)設這個二次函數的頂點為D,與y軸交于點C,它的對稱軸與x軸交于點E,連接AD、DE和DB,當△AOC與△DEB相似時,求這個二次函數的表達式。
[提示:如果一個二次函數的圖象與x軸的交點為 A,那么它的表達式可表示為:
A,那么它的表達式可表示為: ]
]
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,△ABC中,AB=BC,AC=8,tanA=k,P為AC邊上一動點,設PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)證明:△PCE是等腰三角形;
(2)EM、FN、BH分別是△PEC、△AFP、△ABC的高,用含x和k的代數式表示EM、FN,并探究EM、FN、BH之間的數量關系;
(3)當k=4時,求四邊形PEBF的面積S與x的函數關系式.x為何值時,S有最大值?并求出S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
直線 與x、y軸分別交于點A、C.拋物線的圖象經過A、C和點B(1,0).
與x、y軸分別交于點A、C.拋物線的圖象經過A、C和點B(1,0).
(1)求拋物線的解析式;
(2)在直線AC上方的拋物線上有一動點D,當D與直線AC的距離DE最大時,求出點D的坐標,并求出最大距離是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com