
【題目】暑假期間,小明和父母一起開車到距家200千米的景點旅游.出發前,汽車油箱內儲油45升;當行駛150千米時,發現油箱剩余油量為30升.
(1)已知油箱內余油量y(升)是行駛路程x(千米)的一次函數,求y與x的函數關系式;
(2)當油箱中余油量少于3升時,汽車將自動報警.如果往返途中不加油,他們能否在汽車報警前回到家?請說明理由.
科目:初中數學 來源: 題型:
【題目】溫州某企業安排65名工人生產甲、乙兩種產品,每人每天生產2件甲或1件乙,甲產品每件可獲利15元.根據市場需求和生產經驗,乙產品每天產量不少于5件,當每天生產5件時,每件可獲利120元,每增加1件,當天平均每件獲利減少2元.設每天安排x人生產乙產品.
(1)根據信息填表
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生產甲產品可獲得的利潤比生產乙產品可獲得的利潤多550元,求每件乙產品可獲得的利潤.
(3)該企業在不增加工人的情況下,增加生產丙產品,要求每天甲、丙兩種產品的產量相等.已知每人每天可生產1件丙(每人每天只能生產一件產品),丙產品每件可獲利30元,求每天生產三種產品可獲得的總利潤W(元)的最大值及相應的x值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形的頂點A(1,1)、B(3,1),規定把等邊△ABC“先沿x軸翻折,再向左平移1個單位”為一次變換,如果這樣連續經過2018次變換后,等邊△ABC的頂點C的坐標為_____.
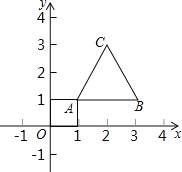
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,O為AC的中點,過點O的直線分別與AB,CD交于點E,F,連接BF交AC于點M,連接DE,BO.若∠COB=60°,FO=FC,則下列結論:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四邊形EBFD是菱形;④MB∶OE=3∶2.其中正確結論的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
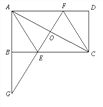
【題目】如圖,在平行四邊形ABCD中,點O是AC中點,AC=2AB,延長AB到G,使BG=AB,連接GO并延長,分別交BC于點E,交AD于點F.
(1)求證:△ABC≌△AOG;
(2)若ABCD為矩形,則四邊形AECF是什么特殊四邊形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
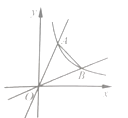
【題目】如圖,在平面直角坐標系中,反比例函數![]() (x>0)與正比例函數y=kx、
(x>0)與正比例函數y=kx、 ![]() (k>1)的圖象分別交于點A、B,若∠AOB=45°,則△AOB的面積是________.
(k>1)的圖象分別交于點A、B,若∠AOB=45°,則△AOB的面積是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
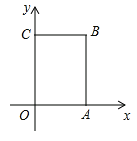
【題目】如圖,在長方形![]() 中,
中,![]() 為平面直角坐標系的原點,點
為平面直角坐標系的原點,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,點
軸上,點![]() 在第一象限內,點
在第一象限內,點![]() 從原點出發,以每秒
從原點出發,以每秒![]() 個單位長度的速度沿著
個單位長度的速度沿著![]() 的路線移動(即沿著長方形的邊移動一周).
的路線移動(即沿著長方形的邊移動一周).
(1)分別求出![]() ,
,![]() 兩點的坐標;
兩點的坐標;
(2)當點![]() 移動了
移動了![]() 秒時,求出點
秒時,求出點![]() 的坐標;
的坐標;
(3)在移動過程中,當三角形![]() 的面積是
的面積是![]() 時,求滿足條件的點
時,求滿足條件的點![]() 的坐標及相應的點
的坐標及相應的點![]() 移動的時間.
移動的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,二次函數y=(x-a)(x-3)(0<a<3)的圖象與x軸交于點A、B(點A在點B的左側),與y軸交于點D,過其頂點C作直線CP⊥x軸,垂足為點P,連接AD、BC.
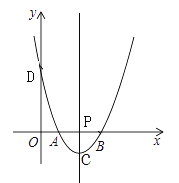
(1)求點A、B、D的坐標;
(2)若△AOD與△BPC相似,求a的值;
(3)點D、O、C、B能否在同一個圓上,若能,求出a的值,若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com