Question

【題目】如圖，拋物線C1：的頂點為A，與x軸的正半軸交于點B．

（1）將拋物線C1上的點的橫坐標和縱坐標都擴大到原來的2倍，求變換后得到的拋物線的解析式；

（2）將拋物線C1上的點（x，y）變為（kx，ky）（|k|＞1），變換后得到的拋物線記作C2，拋物線C2的頂點為C，點P在拋物線C2上，滿足S△PAC=S△ABC，且∠APC=90°．

①當k＞1時，求k的值；

②當k＜﹣1時，請直接寫出k的值，不必說明理由．

Answer 1

【答案】（1）；（2）①k=；②k=．

【解析】

試題分析：（1）由拋物線C1解析式求出A、B及原點坐標，將三點坐標都擴大到原來的2倍，待定系數求解可得；

（2）①如圖1中，當k＞1時，與（1）同理可得拋物線C2的解析式為及頂點C的坐標，根據S△PAC=S△ABC知BP∥AC，繼而可得△ABO是邊長為2的正三角形，四邊形CEBP是矩形，表示出點P的坐標，將其代入到拋物線C2解析式可求得k的值；

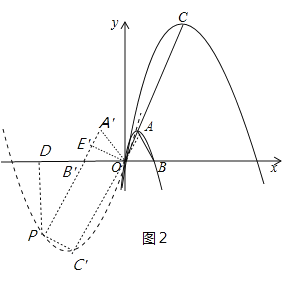
②如圖2中，當k＜﹣1時，作△ABO關于y軸對稱的△A′B′O，OE′⊥A′B′，同理可得四邊形CEBP是矩形，先求出拋物線C2解析式，表示出點P的坐標，將其代入到拋物線C2解析式可求得k的值；

試題解析：（1）∵=，∴拋物線C1經過原點O，點A（1，）和點B（2，0）三點，∴變換后的拋物線經過原點O，（2，）和（4，0）三點，∴變換后拋物線的解析式為；

（2）①如圖1中，當k＞1時，∵拋物線C2經過原點O，（k，k），（2k，0）三點，∴拋物線C2的解析式為，∴O、A、C三點共線，且頂點C為（k，k），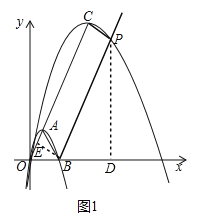

如圖，∵S△PAC=S△ABC，∴BP∥AC，過點P作PD⊥x軸于D，過點B作BE⊥AO于E，由題意知△ABO是邊長為2的正三角形，四邊形CEBP是矩形，∴OE=1，CE=BP=2k﹣1，∵∠PBD=60°，∴BD=，PD=（2k﹣1），∴P（k+，（2k﹣1）），∴（2k﹣1）=，解得：k=；

②如圖2中，當k＜﹣1時，∵拋物線C2經過原點O，（k，k），（2k，0）三點，∴拋物線C2的解析式為，∴O、A、C′三點共線，且頂點C′為（k，k），作△ABO關于y軸對稱的△A′B′O，OE′⊥A′B′，∵S△PAC′=S△ABC=S△AC′B′，∴A′P∥AC′，由題意四邊形PC′OE′是矩形，∴PE′=OC′=﹣2k，B′E′=1，PB′=﹣2k﹣1，在RT△PDB′中，∵∠PDB′=90°，∠PB′D=∠A′B′O=60°，∴DB′=PB′=，DP=（﹣2k﹣1），∴點P坐標[，（2k+1）]，∴（2k+1）=，∴k=．