
已知:如圖所示,關于 的拋物線
的拋物線 與
與 軸交于點
軸交于點 、點
、點 ,與
,與 軸交于點
軸交于點 .
.
(1)求出此拋物線的解析式,并寫出頂點坐標;
(2)在拋物線上有一點 ,使四邊形
,使四邊形 為等腰梯形,寫出點
為等腰梯形,寫出點 的坐標,并求出直線
的坐標,并求出直線 的解析式;
的解析式;
(3)在(2)中的直線 交拋物線的對稱軸于點
交拋物線的對稱軸于點 ,拋物線上有一動點
,拋物線上有一動點 ,
, 軸上有一動點
軸上有一動點 .是否存在以
.是否存在以 為頂點的平行四邊形?如果存在,請直接寫出點
為頂點的平行四邊形?如果存在,請直接寫出點 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.

解析試題考查知識點:拋物線的性質及求解析式,直線求解析式,動點問題
思路分析:
具體解答過程:
(1)∵關于 的拋物線y=ax2+x+c與
的拋物線y=ax2+x+c與 軸交于點A(-2,0)、B(6,0)點
軸交于點A(-2,0)、B(6,0)點
∴把x=-2、y=0和x=6、y=0分別代入到y=ax2+x+c可得方程組 解之得:a=-
解之得:a=-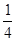 ,c=3
,c=3
∴此拋物線的解析式為:y=-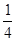 x2+x+3
x2+x+3
根據拋物線頂點坐標的計算方法,可知:
橫坐標:-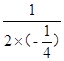 =2;縱坐標:
=2;縱坐標: =4
=4
∴拋物線的頂點坐標為(2,4)
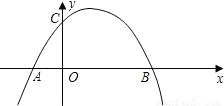
(2)、如圖所示。
過C點做直線CD∥x軸,交拋物線于D,連接AC、BD,則CD兩點的縱坐標應該是一樣的;根據拋物線的對稱性,四邊形ABCD必為等腰梯形。
對于y=-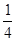 x2+x+3,令x=0,則y=3,故知點C的坐標為(0,3);再令y=3,可得-
x2+x+3,令x=0,則y=3,故知點C的坐標為(0,3);再令y=3,可得-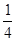 x2+x+3=3,解之得:x=0或4
x2+x+3=3,解之得:x=0或4
∴D點坐標為D(4,3)
設過A(-2,0),D(4,3)兩點的直線解析式為y=kx+b。把x=-2,y=0和x=4,y=3分別代入到y=kx+b中解方程組: 解之得:k=
解之得:k= ,b=1
,b=1
∴直線AD的解析式為y= x+1
x+1
(3)、存在。如下面(A)~(D)圖所示,大致有四種情況。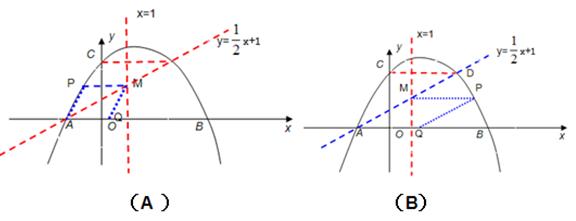
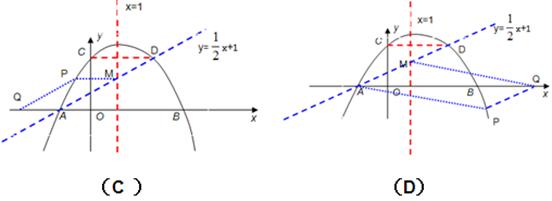
經計算,在圖(A)中,Q點的坐標為:(2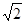 -2,0);在圖(B)中,Q點的坐標為:(6-2
-2,0);在圖(B)中,Q點的坐標為:(6-2 ,0);在圖(C)中,Q點的坐標為:(-2
,0);在圖(C)中,Q點的坐標為:(-2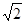 -2,0);在圖(D)中,Q點的坐標為:(6+2
-2,0);在圖(D)中,Q點的坐標為:(6+2 ,0)
,0)
試題點評: 這是一道以拋物線為主導的綜合題目。


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:初中數學 來源: 題型:
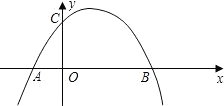 .是否存在以A、M、P、Q為頂點的平行四邊形?如果存在,請直接寫出點Q的坐標;如果不存在,請說明理由.
.是否存在以A、M、P、Q為頂點的平行四邊形?如果存在,請直接寫出點Q的坐標;如果不存在,請說明理由.查看答案和解析>>
科目:初中數學 來源:內蒙古自治區模擬題 題型:解答題
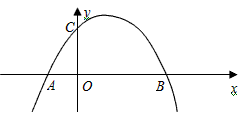
查看答案和解析>>
科目:初中數學 來源:2012-2013學年浙江省杭州市蕭山區九年級(上)段考數學試卷(1-2章)(解析版) 題型:解答題
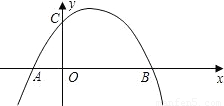
查看答案和解析>>
科目:初中數學 來源:第23章《二次函數與反比例函數》中考題集(33):23.5 二次函數的應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2010年云南省楚雄州雙柏縣中考數學模擬試卷(雨龍中學)(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com