
【題目】觀察下列兩個等式:![]() ,
,![]() ,給出定義如下:我們稱使等式
,給出定義如下:我們稱使等式![]() 成立的一對有理數
成立的一對有理數![]() 為“理想有理數對”,記為
為“理想有理數對”,記為![]() ,如:數對
,如:數對![]() 、
、![]() 都是“理想有理數對”.
都是“理想有理數對”.
(1)數對![]() 、
、![]() 中是“理想有理數對”的是______;
中是“理想有理數對”的是______;
(2)若![]() 是“理想有理數對”,求a的值;
是“理想有理數對”,求a的值;
(3)若![]() 是“理想有理數對”,則
是“理想有理數對”,則![]() ______“理想有理數對”(填“是”、“不是”或“不確定”);
______“理想有理數對”(填“是”、“不是”或“不確定”);
(4)請再寫出一對符合條件的“理想有理數對”.(不能與題目中已有的數對重復).
 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】已知,![]() 、
、![]() 在數軸上對應的數分別用
在數軸上對應的數分別用![]() 、
、![]() 表示,且
表示,且![]() .
.
![]()
(1)數軸上點![]() 表示的數是________,點
表示的數是________,點![]() 表示的數是___________;
表示的數是___________;
(2)若一動點![]() 從點
從點![]() 出發,以
出發,以![]() 個單位長度秒速度由
個單位長度秒速度由![]() 向
向![]() 運動;動點
運動;動點![]() 從原點
從原點![]() 出發,以
出發,以![]() 個單位長度
個單位長度![]() 秒速度向
秒速度向![]() 運動,點
運動,點![]() 、
、![]() 同時出發,點
同時出發,點![]() 運動到
運動到![]() 點時兩點同時停止.設點
點時兩點同時停止.設點![]() 運動時間為
運動時間為![]() 秒.
秒.
①若![]() 從
從![]() 到
到![]() 運動,則
運動,則![]() 點表示的數為_______,
點表示的數為_______,![]() 點表示的數為___________(用含
點表示的數為___________(用含![]() 的式子表示)
的式子表示)
②當![]() 為何值時,點
為何值時,點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() 個單位長度.
個單位長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
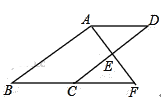
【題目】如圖,E是ABCD的邊CD的中點,延長AE交BC的延長線于點F.
(1)求證:△ADE≌△FCE;
(2)若AB⊥AF,BC=12,EF=6,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖的正方形網格中,每個小正方形的邊長都是單位1,直線a與直線b交于點O,△ABC的頂點均在格點上.
(1)△ABC向右平移 個單位長度到△A1B1C1位置;
(2)對△ABC分別作下列變換:
① 畫出△ABC關于直線a對稱的△A2B2C2;
② 將△ABC繞點O旋轉180°,畫出旋轉后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中,
① △ 與△ 成軸對稱,對稱軸是直線 ;
② △ 與△ 成中心對稱,并在圖中標出對稱中心D的位置.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是∠AOB外的一點,點M,N分別是∠AOB兩邊上的點,點P關于OA的對稱點Q恰好落在線段MN上,點P關于OB的對稱點R落在MN的延長線上.若PM=3cm,PN=4cm,MN=4.5cm,則線段QR的長為( )
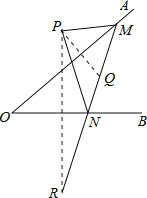
A.4.5 B.5.5 C.6.5 D.7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料
材料1:對稱,也許是中國人最喜歡的。建筑師梁思成曾說過:“無論東方、西方,再沒有一個民族對中軸對稱線如此鐘愛與恪守。”放眼中國的建筑,無論是宮殿、廟宇、亭臺、樓閣、園林無不有著對稱之美。數學世界也里有一些正整數你無論從左往右看,還是從右往左看,數字都是完全一樣的,例如:11、101、2332、1234321、…,像這樣的數我們叫它“對稱數”.
材料2:如果一個三位數![]() ,滿足a+b+c=8,我們就稱這個三位數為“發財數”.
,滿足a+b+c=8,我們就稱這個三位數為“發財數”.
(1)請直接寫出既是“對稱數”又是“發財數”的所有三位數;
(2)一個三位“對稱數”十位數字為7,它的各數位上的數字之和是一個自然數的平方,求這個三位數(請寫出必要的推理過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,AB=5cm,BC=3cm,,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1cm,設出發的時間為t秒.

(1)出發2秒后,求△ABP的周長.
(2)問t為何值時,△BCP為等腰三角形?
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒2cm,若P、Q兩點同時出發,當P、Q中有一點到達終點時,另一點也停止運動.當t為何值時,直線PQ把△ABC的周長分成相等的兩部分?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從①![]() ,②
,②![]() ,③
,③![]() 三個條件中選出兩個作為已知條件,另一個作為結論可以組成3個命題.
三個條件中選出兩個作為已知條件,另一個作為結論可以組成3個命題.

(1)這三個命題中,真命題的個數為________;
(2)選擇一個真命題,并且證明.(要求寫出每一步的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A,B兩點在數軸上對應的數分別為a,b,且點A在點B的左邊,|a|=10,a+b=80,ab<0.
(1)求出a,b的值;
(2)現有一只電子螞蟻P從點A出發,以3個單位長度/秒的速度向右運動,同時另一只電子螞蟻Q從點B出發,以2個單位長度/秒的速度向左運動.
①設兩只電子螞蟻在數軸上的點C相遇,求出點C對應的數是多少?
②經過多長時間兩只電子螞蟻在數軸上相距20個單位長度?
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com