
【題目】如圖,已知⊙![]() 的半徑為
的半徑為![]() ,
, ![]() 為直徑,
為直徑, ![]() 為弦.
為弦. ![]() 與
與![]() 交于點
交于點![]() ,將
,將![]() 沿著
沿著![]() 翻折后,點
翻折后,點![]() 與圓心
與圓心![]() 重合,延長
重合,延長![]() 至
至![]() ,使
,使![]() ,鏈接
,鏈接![]() .
.
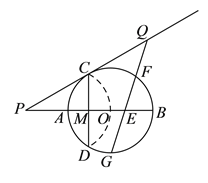
(![]() )求
)求![]() 的長.
的長.
(![]() )求證:
)求證: ![]() 是⊙
是⊙![]() 的切線.
的切線.
(![]() )點
)點![]() 為
為![]() 的中點,在
的中點,在![]() 延長線上有一動點
延長線上有一動點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() (
(![]() 與
與![]() 、
、![]() 不重合).則
不重合).則![]() 為一定值.請說明理由,并求出該定值.
為一定值.請說明理由,并求出該定值.
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() ,理由見解析.
,理由見解析.
【解析】試題分析:(1)連接OC,根據翻折的性質求出OM,CD⊥OA,再利用勾股定理列式求解即可;(2)利用勾股定理列式求出PC,然后利用勾股定理逆定理求出∠PCO=90°,再根據圓的切線的定義證明即可;(3)連接GA、AF、GB,根據等弧所對的圓周角相等可得∠BAG=∠AFG,然后根據兩組角對應相等兩三角相似求出△AGE和△FGA相似,根據相似三角形對應邊成比例可得![]() ,從而得到GEGF=AG2,再根據等腰直角三角形的性質求解即可.
,從而得到GEGF=AG2,再根據等腰直角三角形的性質求解即可.
(![]() )連接
)連接![]() ,
,

∵![]() 沿
沿![]() 翻折后,
翻折后, ![]() 與
與![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是⊙
是⊙![]() 的切線.
的切線.
(![]() )
)![]() ,
, ![]() 為定值,
為定值,
連接![]() ,
, ![]() ,
, ![]() ,
,

∵點![]() 為
為![]() 的中點,
的中點,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 為直徑,
為直徑, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】閱讀材料,并回答問題
如圖,有一根木棒MN放置在數軸上,它的兩端M、N分別落在點A、B.將木棒在數軸上水平移動,當點M移動到點B時,點N所對應的數為20,當點N移動到點A時,點M所對應的數為5.
![]() (單位:cm)
(單位:cm)
由此可得,木棒長為__________cm.
借助上述方法解決問題:
一天,美羊羊去問村長爺爺的年齡,村長爺爺說:“我若是你現在這么大,你還要40年才出生呢,你若是我現在這么大,我已經是老壽星了,116歲了,哈哈!”美羊羊納悶,村長爺爺到底是多少歲?
(1)請你畫出示意圖,求出村長爺爺和美羊羊現在的年齡.
(2)若羊村中的小羊均與美羊羊同歲,老羊均與村長爺爺同歲。灰太狼計劃為全家抓5只羊,綜合考慮口感和生長周期等因素,決定所抓羊的年齡之和不超過112歲且高于34歲。請問灰太狼有幾種抓羊方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
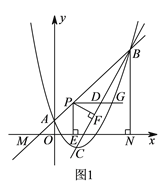
【題目】如圖![]() ,二次函數
,二次函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象交于
的圖象交于![]() ,
, ![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在第一象限內,點
在第一象限內,點![]() 是二次函數圖象的頂點,點
是二次函數圖象的頂點,點![]() 是一次函數
是一次函數![]() 的圖象與
的圖象與![]() 軸的交點,過點
軸的交點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,且
,且![]() .
.
(![]() )求直線
)求直線![]() 和直線
和直線![]() 的解析式.
的解析式.
(2)點![]() 是線段
是線段![]() 上一點,點
上一點,點![]() 是線段
是線段![]() 上一點,
上一點, ![]() 軸,射線
軸,射線![]() 與拋物線交于點
與拋物線交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,
, ![]() 于點
于點![]() ,當
,當![]() 與
與![]() 的乘積最大時,在線段
的乘積最大時,在線段![]() 上找一點
上找一點![]() (不與點
(不與點![]() ,點
,點![]() 重合),使
重合),使![]() 的值最小,求點
的值最小,求點![]() 的坐標和
的坐標和![]() 的最小值.
的最小值.
(![]() )如圖
)如圖![]() ,直線
,直線![]() 上有一點
上有一點![]() ,將二次函數
,將二次函數![]() 沿直線
沿直線![]() 平移,平移的距離是
平移,平移的距離是![]() ,平移后拋物線使點
,平移后拋物線使點![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]() ,點
,點![]() ;當
;當![]() 是直角三角形時,求t的值.
是直角三角形時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區為了綠化環境,計劃分兩次購進![]() 、
、![]() 兩種花草,第一次分別購進
兩種花草,第一次分別購進![]() 、
、![]() 兩種花草
兩種花草![]() 棵和
棵和![]() 棵,共花費
棵,共花費![]() 元;第二次分別購進
元;第二次分別購進![]() 、
、![]() 兩種花草
兩種花草![]() 棵和
棵和![]() 棵.兩次共花費
棵.兩次共花費![]() 元(兩次購進的
元(兩次購進的![]() 、
、![]() 兩種花草價格均分別相同).
兩種花草價格均分別相同).
(![]() )
)![]() 、
、![]() 兩種花草每棵的價格分別是多少元?
兩種花草每棵的價格分別是多少元?
(![]() )若購買
)若購買![]() 、
、![]() 兩種花草共
兩種花草共![]() 棵,且
棵,且![]() 種花草的數量少于
種花草的數量少于![]() 種花草的數量的
種花草的數量的![]() 倍,請你給出一種費用最省的方案,并求出該方案所需費用.
倍,請你給出一種費用最省的方案,并求出該方案所需費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
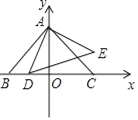
【題目】如圖,在平面直角坐標系中,點A(0,2),B(﹣2,0),點D是x軸上一個動點,以AD為一直角邊在一側作等腰直角三角形ADE,∠DAE=90°,若△ABD為等腰三角形時點E的坐標為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一艘輪船和一艘快艇沿相同路線從甲港出發到乙港,行駛過程隨時間變化的圖象如圖所示,下列結論錯誤的是( )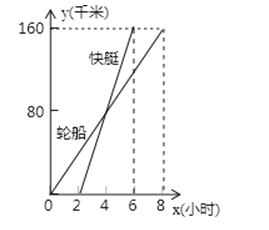
A.輪船的速度為20千米/小時
B.快艇的速度為![]() 千米/小時
千米/小時
C.輪船比快艇先出發2小時
D.快艇比輪船早到2小時
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com