
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上的動點(點
上的動點(點![]() 與點
與點![]() 、
、![]() 不重合),過點
不重合),過點![]() 作
作![]() 交射線
交射線![]() 于點
于點![]() ,聯結
,聯結![]() ,點
,點![]() 是
是![]() 的中點,過點
的中點,過點![]() 、
、![]() 作直線,交
作直線,交![]() 于點
于點![]() ,聯結
,聯結![]() 、
、![]() .
.
(1)當點![]() 在邊
在邊![]() 上,設
上,設![]() ,
,![]() .
.
①寫出![]() 關于
關于![]() 的函數關系式及定義域;
的函數關系式及定義域;
②判斷![]() 的形狀,并給出證明;
的形狀,并給出證明;
(2)如果![]() ,求
,求![]() 的長.
的長.

【答案】(1)①![]() ;②詳見解析;(2)
;②詳見解析;(2)![]() 或
或![]()
【解析】
(1)①先證△DEB為等腰直角三角形,設DB=x,CE=y知EB=![]() x,由EB+CE=4知
x,由EB+CE=4知![]() x+y=4,從而得出答案;
x+y=4,從而得出答案;
②由∠ADE=90°,點F是AE的中點知CF=AF=![]() AE,DF=AF=
AE,DF=AF=![]() AE,據此得出CF=DF,再由∠CFE=2∠CAE,∠EFD=2∠EAD知∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD,結合∠CAB=45°知∠CFD=90°,據此可得答案;
AE,據此得出CF=DF,再由∠CFE=2∠CAE,∠EFD=2∠EAD知∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD,結合∠CAB=45°知∠CFD=90°,據此可得答案;
(2)分點E在BC上和BC延長線上兩種情況,分別求出DF、GF的長,從而得出答案.
(1)①∵![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
②![]() ,
,![]() ,
,
![]() ,
,
![]() 點
點![]() 是
是![]() 的中點,
的中點,
![]() ,
,![]() ,
,
![]() ,∠CAF=∠ACF,∠EAD=∠FDA,
,∠CAF=∠ACF,∠EAD=∠FDA,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形;
是等腰直角三角形;
(2)如圖![]() ,當點
,當點![]() 在
在![]() 上時,
上時,![]() ,
,![]() ,
,
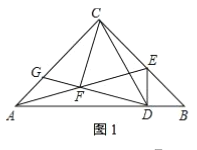
在![]() 中,
中,![]() ,
,
則![]() ,
,
∴sin∠CAE=![]()
![]() ,
,
又![]() ,
,
由(2)得:![]() ,
,
∴∠CFG=90°,
∴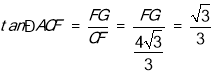
∴![]() ,
,
![]() ;
;
如圖![]() ,當點
,當點![]() 在
在![]() 延長線上時,
延長線上時,![]() ,
,
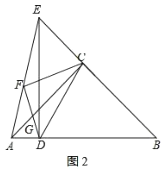
同理可得![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
綜上所述:DG的長為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在![]() 的網格紙中,每個小正方形的邊長都為1,動點
的網格紙中,每個小正方形的邊長都為1,動點![]() ,
,![]() 分別從點
分別從點![]() ,點
,點![]() 同時出發向右移動,點
同時出發向右移動,點![]() 的運動速度為每秒2個單位,點
的運動速度為每秒2個單位,點![]() 的運動速度為每秒1個單位,當點
的運動速度為每秒1個單位,當點![]() 運動到點
運動到點![]() 時,兩個點同時停止運動.
時,兩個點同時停止運動.

(1)當運動時間![]() 為3秒時,請在網格紙圖中畫出線段
為3秒時,請在網格紙圖中畫出線段![]() ,并求其長度.
,并求其長度.
(2)在動點![]() ,
,![]() 運動的過程中,若
運動的過程中,若![]() 是以
是以![]() 為腰的等腰三角形,求相應的時刻
為腰的等腰三角形,求相應的時刻![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
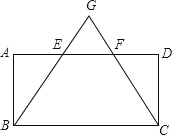
【題目】如圖,在平行四邊形ABCD中,E、F為AD上兩點,AE=EF=FD,連接BE、CF并延長,交于點G, GB=GC.
(1)求證:四邊形ABCD是矩形;
(2)若△GEF的面積為2.
①求四邊形BCFE的面積;
②四邊形ABCD的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年3月,某集團隨機抽取所屬的m家商業連鎖店進行評估,將各連鎖店按照評估成績分成了A、B、C、D四個等級,繪制了如圖尚不完整的統計圖表.
評估成績 | 評定等級 | 頻數 |
| A | 2 |
| B | b |
| C | 15 |
| D | 6 |
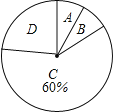
根據以上信息解答下列問題:
(1)求m,b的值;
(2)在扇形統計圖中,求B等級所在扇形的圓心角的大小;
(3)從評估成績不少于80分的連鎖店中,任選2家介紹營銷經驗,用樹狀圖或列表法求其中至少有一家是A等級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了預防“流感”,某學校在休息日用“藥熏”消毒法對教室進行消毒.已知藥物釋放過程中,室內每立方米的含藥量y(毫克)與時間x(時)成正比例;藥物釋放結束后,y與x成反比例;如圖所示,根據圖中提供的信息,解答下列問題:
(1)寫出從藥物釋放開始,y與x之間的兩個函數解析式;
(2)據測定,當藥物釋放結束后,每立方米的含藥量降至0.25毫克以下時,學生方可進入教室,那么從藥物釋放開始,至少需要經過多長時間,學生才能進入教室?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),![]() ,
,![]() ,
,![]() 垂足分別為
垂足分別為![]() 、
、![]() ,
,![]() .點
.點![]() 在線段
在線段![]() 上以
上以![]() 的速度由點
的速度由點![]() 向點
向點![]() 運動,同時點
運動,同時點![]() 在射線
在射線![]() 上運動.它們運動的時間為
上運動.它們運動的時間為![]() (當點
(當點![]() 運動結束時,點
運動結束時,點![]() 運動隨之結束).
運動隨之結束).
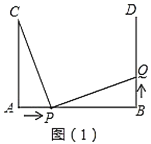
(1)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,當
的運動速度相等,當![]() 時,
時,![]() 與
與![]() 是否全等,并判斷此時線段
是否全等,并判斷此時線段![]() 和線段
和線段![]() 的位置關系,請分別說明理由;
的位置關系,請分別說明理由;
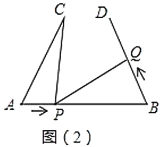
(2)如圖(2),若“![]() ,
,![]() ”改為“
”改為“![]() ”,點
”,點![]() 的運動速度為
的運動速度為![]() ,其它條件不變,當點
,其它條件不變,當點![]() 、
、![]() 運動到何處時有
運動到何處時有![]() 與
與![]() 全等,求出相應的
全等,求出相應的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店用4000元購進一批某品牌的文化衫若干件,很快售完,該店又用6300元錢購進第二批這種文化衫,所進的件數比第一批多40%,每件文化衫的進價比第一批每件文化衫的進價多10元,請解答下列問題:
(1)求購進的第一批文化衫的件數;
(2)為了取信于顧客,在這兩批文化衫的銷售中,售價保持了一致.若售完這兩批文化衫服裝店的總利潤不少于4100元錢,那么服裝店銷售該品牌文化衫每件的最低售價是多少元?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=a(x+m)2的頂點坐標為(﹣1,0),且過點A(﹣2,﹣![]() ).
).
(1)求這個二次函數的解析式;
(2)點B(2,﹣2)在這個函數圖象上嗎?
(3)你能通過左,右平移函數圖象,使它過點B嗎?若能,請寫出平移方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com