

 ×(∠ABC+∠ACB)=90°-α,
×(∠ABC+∠ACB)=90°-α, ;
; ∠ACE,∠DBC=
∠ACE,∠DBC= ∠ABC,
∠ABC, ;
; ×[360°-(∠ABC+∠ACB)]=90°+
×[360°-(∠ABC+∠ACB)]=90°+ ,
, .
.

科目:初中數學 來源: 題型:
 17、如圖,在△ABC中,AB=AC,AD是△ABC的平分線,DE⊥AB,DF⊥AC,垂足分別是E,F.則下面結論中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的點到B、C兩點距離相等;④圖中共有3對全等三角形,正確的有:
17、如圖,在△ABC中,AB=AC,AD是△ABC的平分線,DE⊥AB,DF⊥AC,垂足分別是E,F.則下面結論中①DA平分∠EDF;②AE=AF,DE=DF;③AD上的點到B、C兩點距離相等;④圖中共有3對全等三角形,正確的有:查看答案和解析>>
科目:初中數學 來源: 題型:
 8、如圖,在△ABC中,AB=20cm,AC=12cm,點P從點B出發以每秒3cm的速度向點A運動,點Q從點A同時出發以每秒2cm的速度向點C運動,其中一個動點到達端點時,另一個動點也隨之停止運動,當△APQ是等腰三角形時,運動的時間是( )
8、如圖,在△ABC中,AB=20cm,AC=12cm,點P從點B出發以每秒3cm的速度向點A運動,點Q從點A同時出發以每秒2cm的速度向點C運動,其中一個動點到達端點時,另一個動點也隨之停止運動,當△APQ是等腰三角形時,運動的時間是( )查看答案和解析>>
科目:初中數學 來源: 題型:
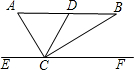 如圖,Rt△ABC中,DC是斜邊AB上的中線,EF過點C且平行于AB.若∠BCF=35°,則∠ACD的度數是( )
如圖,Rt△ABC中,DC是斜邊AB上的中線,EF過點C且平行于AB.若∠BCF=35°,則∠ACD的度數是( )| A、35° | B、45° | C、55° | D、65° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com