
【題目】如圖,菱形OABC的頂點A的坐標為(3,4),頂點C在x軸的正半軸上,反比例函數y= ![]() (x>0)的圖象經過頂點B,則反比例函數的表達式為( )
(x>0)的圖象經過頂點B,則反比例函數的表達式為( ) 
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
【答案】C
【解析】 解:過A作AM⊥x軸于M,過B作BN⊥x軸于N,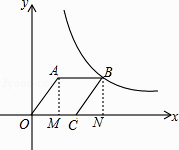
則∠AMO=∠BNC=90°,
∵四邊形AOCB是菱形,
∴OA=BC=AB=OC,AB//OC,OA//BC,
∴∠AOM=∠BCN,
∵A(3,4),
∴OM=3,AM=4,由勾股定理得:OA=5,
即OC=OA=AB=BC=5,
在△AOM和△BCN中
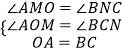
∴△AOM≌△BCN(AAS),
∴BN=AM=4,CN=OM=3,
∴ON=5+3=8,
即B點的坐標是(8,4),
把B的坐標代入y= ![]() 得:k=32,
得:k=32,
即y= ![]() ,
,
故選:C.
【考點精析】利用菱形的性質對題目進行判斷即可得到答案,需要熟知菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形AOCB的邊長為4,反比例函數y= ![]() (k≠0,且k為常數)的圖象過點E,且S△AOE=3S△OBE .
(k≠0,且k為常數)的圖象過點E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函數圖象與線段BC交于點D,直線y= ![]() x+b過點D與線段AB交于點F,延長OF交反比例函數y=
x+b過點D與線段AB交于點F,延長OF交反比例函數y= ![]() (x<0)的圖象于點N,求N點坐標.
(x<0)的圖象于點N,求N點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以A點為圓心,以相同的長為半徑作弧,分別與射線AM,AN交于B,C兩點,連接BC,再分別以B,C為圓心,以相同長(大于![]() BC)為半徑作弧,兩弧相交于點D,連接AD,BD,CD.若∠MBD=40°,則∠NCD的度數為_____.
BC)為半徑作弧,兩弧相交于點D,連接AD,BD,CD.若∠MBD=40°,則∠NCD的度數為_____.
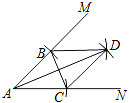
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據有關資料統計,兩個城市之間每天的電話通話次數T與這兩個城市的人口數xy(單位:萬人)以及兩城市間的距離l(單位:km)之間有下列關系式![]() (k為常數) 己知A,B,C三個城市的人口數及它們之間的距離如圖所示如果A,B兩個城市間每天的電話通話次數為n,求B,C兩個城市間每天的電話通話次數(用含n的代數式表示)
(k為常數) 己知A,B,C三個城市的人口數及它們之間的距離如圖所示如果A,B兩個城市間每天的電話通話次數為n,求B,C兩個城市間每天的電話通話次數(用含n的代數式表示)
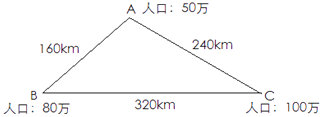
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
①最大的負整數是﹣1;②數軸上表示數2 和﹣2的點到原點的距離相等;③當a≤0時,|a|=﹣a成立;④a的倒數是![]() ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.
A. 2 個 B. 3 個 C. 4 個 D. 5 個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,第一個正方形ABCD的位置如圖所示,點A的坐標為(2,0),點D的坐標為(0,4),延長CB交x軸于點A1,作第二個正方形A1B1C1C;延長C1B1交x軸于點A2,作第三個正方形A2B2C2C1…按這樣的規律進行下去,第2018個正方形的面積為( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】猜想與證明: 如圖,擺放矩形紙片ABCD與矩形紙片ECGF,使B、C、G三點在一條直線上,CE在邊CD上,連接AF,若M為AF的中點,連接DM,EM.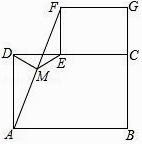
(1)試猜想寫出DM與EM的數量關系,并證明你的結論. 拓展與延伸:
(2)若將“猜想與證明”中的紙片換成正方形紙片ABCD與正方形紙片ECGF,其他條件不變,則(1)中的結論是否仍然成立?請直接寫出你的判斷.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩根旗桿AC與BD相距12m,某人從B點沿AB走向A,一定時間后他到達點M,此時他仰望旗桿的頂點C和D,兩次視線夾角為90°,且CM=DM.已知旗桿AC的高為3m,該人的運動速度為0、5m/s,求這個人走了多長時間?
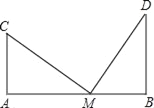
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,lA,lB分別表示A步行與B騎車在同一路上行駛的路程S與時間t的關系.
(1)B出發時與A相距______千米.
(2)B走了一段路后,自行車發生故障,進行修理,所用的時間是______小時.
(3)B出發后______小時與A相遇.
(4)若B的自行車不發生故障,保持出發時的速度前進,______小時與A相遇,相遇點離B的出發點______千米.在圖中表示出這個相遇點C.
(5)求出A行走的路程S與時間t的函數關系式。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com