
【題目】如圖,在△ABC中,∠ABC=∠ACB,以AC為直徑的⊙O分別交AB、BC于點M、N,點P在AB的延長線上,且∠CAB=2∠BCP.
(1)求證:直線CP是⊙O的切線.
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求點B到AC的距離.
,求點B到AC的距離.
(3)在第(2)的條件下,求△ACP的周長.

【答案】(1)證明見解析(2)4(3)20
【解析】解:(1)∵∠ABC=∠ACB且∠CAB=2∠BCP,在△ABC中,∠ABC+∠BAC+∠BCA=180°,
∴2∠BCP+2∠BCA=180°。
∴∠BCP+∠BCA=90°,即∠PCA=90°。
又∵AC是⊙O的直徑,∴直線CP是⊙O的切線。
(2)如圖,作BD⊥AC于點D,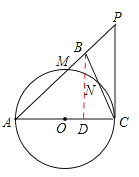
∵PC⊥AC,∴BD∥PC。∴∠PCB=∠DBC。
∵C=2![]() ,sin∠BCP=
,sin∠BCP=![]()
∴![]() ,解得:DC=2。
,解得:DC=2。
∴由勾股定理得:BD=4。∴點B到AC的距離為4。
(3)如圖,連接AN,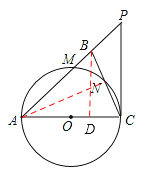
在Rt△ACN中, ,
,
又CD=2,∴AD=AC﹣CD=5﹣2=3。
∵BD∥CP,∴△ABD∽△ACP。
∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
在Rt△ACP中,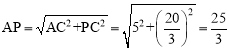 。
。
∴△ACP的周長為![]() 。
。
(1))根據∠ABC=∠AC且∠CAB=2∠BCP,在△ABC中∠ABC+∠BAC+∠BCA=180°,得到2∠BCP+2∠BCA=180°,從而得到∠BCP+∠BCA=90°,證得直線CP是⊙O的切線。
(2)作BD⊥AC于點D,得到BD∥PC,從而利用![]() 求得DC=2,再根據勾股定理求得點B到AC的距離為4。
求得DC=2,再根據勾股定理求得點B到AC的距離為4。
(3)先求出AC的長度,然后由BD∥PC求得△ABD∽△ACP,利用比例線段關系求得CP的長度,再由勾股定理求出AP的長度,從而求得△ACP的周長


科目:初中數學 來源: 題型:
【題目】某電器專賣店策劃五一促銷活動,已知一款電視機的成本價為1800元/臺,專賣店計劃將其打七五折銷售,同時還要保證每臺至少獲得10%的利潤.若設該款電視機的標價為x元/臺,則x滿足的不等關系為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=8cm,對角線AC,BD相交于點O,點E,F分別從B,C兩點同時出發,以1cm/s的速度沿BC,CD運動,到點C,D時停止運動,設運動時間為t(s),△OEF的面積為s(cm2),則s(cm2)與t(s)的函數關系可用圖象表示為( )
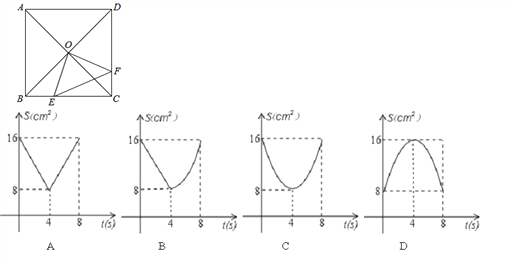
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O 重合),連接AC交射線OE于點D.設∠OAC=x°.
(1)如圖1,若AB∥ON,則∠ABO的度數是;
(2)如圖2,當∠BAD=∠ABD時,試求x的值(要說明理由);
(3)如圖3,若AB⊥OM,則是否存在這樣的x的值,使得△ADB中有兩個相等的角?若存在,直接寫出x的值;若不存在,說明理由.(自己畫圖) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查中,最適合采用全面調查的是( )
A. 調查一批汽車的使用壽命 B. 調查春節聯歡晚會的收視率
C. 調查某航班的旅客是否攜帶違禁物品 D. 調查全國七年級學生的視力情況
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中B(3,2),BC⊥y軸于C,BA⊥x軸于A,點E在線段AB上從B向A以每秒1個單位的速度運動,運動時間為t秒(0<t<2).將BE沿BD折疊,使E點恰好落在BC上的F處.
(1)如圖1,若E為AB的中點,請直接寫出F、D兩點的坐標:F( , ) D( , )
(2)如圖1,連接CD,在(1)的條件下,求證:CD=FD.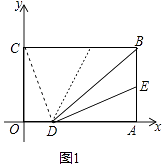
(3)如圖2,在E點運動的同時,M點在OC上從C向O運動,N點在OA上從A向O運動,M的運動速度為每秒3個單位,N的運動速度為每秒a個單位.在運動過程中,△CMF能與△ANE全等嗎?若能,求出此時a與t的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,點E、F分別為長方形紙帶ABCD的邊AD、BC上的點,∠DEF=19°,將紙帶沿EF折疊成圖②(G為ED和EF的交點,再沿BF折疊成圖③(H為EF和DG的交點),則圖③中∠DHF=° 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com