
已知如圖所示,直線![]() 的解析式為
的解析式為![]() ,并且與
,并且與![]() 軸、
軸、![]() 軸分別相交于點A、B。
軸分別相交于點A、B。
(1)求A、B兩點的坐標;
(2)一個圓心在坐標原點、半徑為1的圓,以0.4個單位/每秒的速度向![]() 軸正方向運動,問什么時刻該圓與直線
軸正方向運動,問什么時刻該圓與直線![]() 相切;
相切;
(3)在題(2)中,若在圓開始運動的同時,一動點P從B點出發,沿BA方向以0.5個單位/秒的速度運動,問在整個運動的過程中,點P在動圓的圓面(圓上和圓的內部)上一共運動了多少時間?

解:(1)在![]() 中,令
中,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
故得A、B兩點的坐標為A(4,0),B(0,-3)
(2)若動圓的圓心在C處時與直線相切。設切點為D,如圖所示。

連接CD,則CD⊥AD
由∠CAD=∠BAO,∠CDA=∠BOA=Rt∠,可知Rt△ACD∽Rt△ABO
∴![]() ,即
,即![]() ,則
,則![]()
此時![]() ,
,![]() (秒)
(秒)
根據對稱性.圓C還可能在直線的右側,與直線相切。
此時![]() ,
,
![]() (秒) 答:(略)
(秒) 答:(略)
(3)設在![]() 秒,動圓的圓心在F點處,動點在P處,此時OF=0.4
秒,動圓的圓心在F點處,動點在P處,此時OF=0.4![]() ,BP=0.5
,BP=0.5![]() ,F點的坐標為(0.4
,F點的坐標為(0.4![]() ,0),連接PF。
,0),連接PF。
∵![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴FP∥OB, ∴PF⊥OA
∴P點的橫坐標為0.4![]() ,又∵P點在直線AB上,∴P點的縱坐標為0.3
,又∵P點在直線AB上,∴P點的縱坐標為0.3![]() -3,
-3,
可見:當PF=1時,P點在動圓上,當![]() 時,P點在動圓內。
時,P點在動圓內。
當P=1時,由對稱性可知,有兩種情況:
①當P點在![]() 軸下方時,
軸下方時,![]() ,解之得:
,解之得:![]()
②當P點在![]() 軸上方時,
軸上方時,![]() ,解之得:
,解之得:![]()
∴當![]() 時,
時,![]() ,此時點P在動圓的圓面上,所經過的時間為
,此時點P在動圓的圓面上,所經過的時間為![]() ,
,
答:動點在動圓的圓面上共經過了![]() 秒。
秒。


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
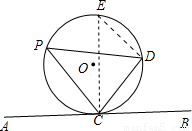
 22、定義:弦切角:頂點在圓上,一邊與圓相交,另一邊和圓相切的角叫弦切角.
22、定義:弦切角:頂點在圓上,一邊與圓相交,另一邊和圓相切的角叫弦切角.查看答案和解析>>
科目:初中數學 來源:2008-2009學年西部地區九年級(上)第二次月考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com