
【題目】如圖,已知△ABC為等邊三角形,點D,E分別在邊AB、AC上,AD=AE,連接DC,點M,P,N分別為DE,DC,BC的中點.
(1)觀察猜想
在如圖中,線段PM與PN的數量關系是______,∠MPN的度數是______;
(2)探究證明
把△ADE繞點A逆時針方向旋轉到如圖的位置,
①判斷△PMN的形狀,并說明理由;
②求∠MPN的度數;
(3)拓展延伸
若△ABC為直角三角形,∠BAC=90°,AB=AC=12,點DE分別在邊AB,AC上,AD=AE=4,連接DC,點M,P,N分別為DE,DC,BC的中點.把△ADE繞點A在平面內自由旋轉,如圖.
①△PMN的是______三角形.
②直接利用①中的結論,求△PMN面積的最大值.
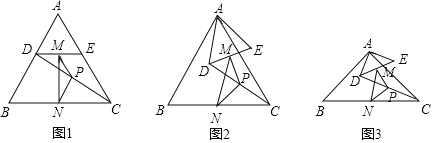
【答案】(1)PM=PN,120°.(2)①△PMN是等腰三角形.證明見解析;②120°.(3)①等腰直角;②32.
【解析】
(1)結論:PM=PN,120°.利用三角形的中位線定理即可解決問題;
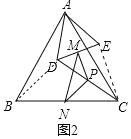
(2)①如圖2中,連接BD、EC.證明△BAD≌△CAE(SAS),可得BD=EC,再利用三角形中位線定理即可解決問題;
②利用三角形的外角以及平行線的性質即可解決問題;
(3)①由(2)可知:△PMN是等腰直角三角形;
②因為PM=PN=![]() BD,推出BD最大時,PM最大,△PMN面積最大.
BD,推出BD最大時,PM最大,△PMN面積最大.
(1)結論:PM=PN,120°.
理由:如圖1中,∵△ABC是等邊三角形,
∴AB=AC,
∵AD=AE,
∴BD=EC,
∵點M,P,N分別為DE,DC,BC的中點,
∴PM=![]() EC,PN=
EC,PN=![]() BD,PM∥AC,PN∥AB,
BD,PM∥AC,PN∥AB,
∴PM=PN,∠MPD=∠ACD,∠PNC=∠B=60°,
∵∠MPN=∠MPD+∠DPN=∠ACD+∠DCB+∠PNC=120°,
故答案為PM=PN,120°;
(2)如圖2中,連接BD、EC,
①∵∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
∵BA=CA,DA=EA,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵點M,P,N分別為DE,DC,BC的中點,
∴PN∥BD,PM∥EC,PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PN=PM,
∴△PMN是等腰三角形;
②∵PN∥BD,PM∥EC,
∴∠PNC=∠DBC,∠DPM=∠A=ECD,
∴∠MPN=∠MPD+∠DPN=∠ECD+∠PNC+∠DCB=∠ECD+∠DCB+∠DBC=∠ACE+∠ACD+∠DCB+∠DBC=∠ABD+∠ACB+∠DBC=∠ACB+∠ABC=120°;
(3)①△PMN是等腰直角三角形;
②∵PM=PN=![]() BD,
BD,
∴BD最大時,PM最大,△PMN面積最大,
∴點D在BA的延長線上,
∴BD=AB+AD=16,∴PM=8,∴S△PMN最大=![]() PM2=
PM2=![]() ×82=32.
×82=32.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
【題目】今年“五一節”前,某商場用60萬元購進某種商品,該商品有甲、乙兩種包裝共500件,其中每件甲包裝中有75個A種產品,每個A產品的成本為12元;每件乙包裝中有100個B產品,每個B種產品的成本為14元.商場將A產品標價定為每個18元,B產品標價定為每個20元.
(1)甲、乙兩種包裝的產品各有多少件?
(2)“五一節”商場促銷,將A產品按原定標價打9折銷售,B種產品按原定標價打8.5折銷售,“五一節”期間該產品全部賣完,該商場銷售該商品共獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,點E在CD上,點F、G在AB上,且AF=FG=BG=DE=CE。以A、B、C、D、E、F、G這7個點中的三個為頂點的三角形中,面積最小的三角形有_________個,面積最大的三角形有__________個。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某生態示范村種植基地計劃用90畝~120畝的土地種植一批葡萄,原計劃總產量要達到36萬斤.
(1)列出原計劃種植畝數y(畝)與平均每畝產量x(萬斤)之間的函數關系式,并寫出自變量x的取值范圍;
(2)為了滿足市場需求,現決定改良葡萄品種.改良后平均每畝產量是原計劃的1.5倍,總產量比原計劃增加了9萬斤,種植畝數減少了20畝,原計劃和改良后的平均每畝產量各是多少萬斤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的《朗讀者》節目激發了同學們的讀書熱情,為了引導學生“多讀書,讀好書”,某校對八年級部分學生的課外閱讀量進行了隨機調查,整理調查結果發現,學生課外閱讀的本數量少的有![]() 本,最多的有
本,最多的有![]() 本,并根據調查結果繪制了不完整的圖表,如下所示:
本,并根據調查結果繪制了不完整的圖表,如下所示:
本數(本) | 頻數(人數) | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|

(![]() )統計圖表中的
)統計圖表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )請將頻數分布直方圖補充完整.
)請將頻數分布直方圖補充完整.
(![]() )求所有被調查學生課外閱讀的平均本數.
)求所有被調查學生課外閱讀的平均本數.
(![]() )若該校八年級共有
)若該校八年級共有![]() 名學生,請你估計該校八年級學生課外閱讀
名學生,請你估計該校八年級學生課外閱讀![]() 本及以上的人數.
本及以上的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種實驗用軌道彈珠,在軌道上行駛5分鐘后離開軌道,前2分鐘其速度v(米/分)與時間t(分)滿足二次函數v=at2,后三分鐘其速度v(米/分)與時間t(分)滿足反比例函數關系,如圖,軌道旁邊的測速儀測得彈珠1分鐘末的速度為2米/分,求:

(1)二次函數和反比例函數的關系式.
(2)彈珠在軌道上行駛的最大速度.
(3)求彈珠離開軌道時的速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
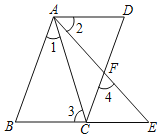
【題目】如圖,已知四邊形ABCD,AB∥CD,點E是BC延長線上一點,連接AC、AE,AE交CD于點F,∠1=∠2,∠3=∠4.
證明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
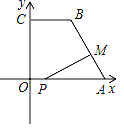
【題目】如圖,在平面直角坐標系中,已知點A(10,0),B(4,8),C(0,8),連接AB,BC,點P在x軸上,從原點O出發,以每秒1個單位長度的速度向點A運動,同時點M從點A出發,以每秒2個單位長度的速度沿折線A﹣B﹣C向點C運動,其中一點到達終點時,另一點也隨之停止運動,設P,M兩點運動的時間為t秒.
(1)求AB長;
(2)設△PAM的面積為S,當0≤t≤5時,求S與t的函數關系式,并指出S取最大值時,點P的位置;
(3)t為何值時,△APM為直角三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某大學公益組織計劃購買![]() 兩種的文具套裝進行捐贈,關注留守兒童經洽談,購買
兩種的文具套裝進行捐贈,關注留守兒童經洽談,購買![]() 套裝比購買
套裝比購買![]() 套裝多用20元,且購買5套
套裝多用20元,且購買5套![]() 套裝和4套
套裝和4套![]() 套裝共需820元.
套裝共需820元.
(1)求購買一套![]() 套裝文具、一套
套裝文具、一套![]() 套裝各需要多少元?
套裝各需要多少元?
(2)根據該公益組織的募捐情況和捐助對象情況,需購買![]() 兩種套裝共60套,要求購買
兩種套裝共60套,要求購買![]() 兩種套裝的總費用不超過5240元,則購買
兩種套裝的總費用不超過5240元,則購買![]() 套裝最多多少套?
套裝最多多少套?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com