閱讀快車系列答案科目：初中數學 來源： 題型：
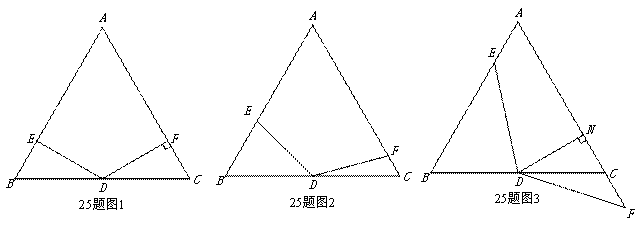
在△ABC中，AB=AC，∠A=60°，點D是線段BC的中點，∠EDF=120°，DE與線段AB相交于點E，DF與線段AC（或AC的延長線）相交于點F.
（1）如圖1，若DF⊥AC，垂足為F，AB=4，求BE的長；
（2）如圖2，將（1）中的∠EDF繞點D順時針旋轉一定的角度，DF扔與線段AC相交于點F.求證：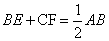
；
（3）如圖3，將（2）中的∠EDF繼續繞點D順時針旋轉一定的角度，使DF與線段AC的延長線交與點F，作DN⊥AC于點N，若DN=FN，求證：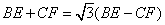
.
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知反比例函數y＝
與一次函數y＝k2x＋b的圖象交于點A(1，8)、B(－4，m)．
(1)求k1、k2、b的值；
(2)求△AOB的面積；
(3)若M(x1，y1)、N(x2，y2)是比例函數y＝圖象上的兩點，且x1＜x2，y1＜y2，指出點M、N各位于哪個象限，并簡要說明理由．
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
把代數式3x3 –12x2+12x分解因式，結果正確的是（ ）
A.3x(x2–4x+4) B. 3x (x–4)2
C. 3x(x+2)(x–2) D. 3x (x–2)2
查看答案和解析>>
科目：初中數學 來源： 題型：
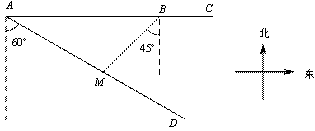
如圖，某市對位于筆直公路AC上兩個小區A、B的供水路線進行優化改造，供水站M在筆直公路AD上，測得供水站M在小區A的南偏東60°方向，在小區B的西南方向，小區A、B之間的距離為300(
+1)米，求供水站M分別到小區A、B的距離。（結果可保留根號）
|
查看答案和解析>>
科目：初中數學 來源： 題型：
如果一種變換是將拋物線向右平移2個單位或向上平移1個單位，我們把這種變換稱為拋物線的簡單變換。已知拋物線經過兩次簡單變換后的一條拋物線是
，則原拋物線的解析式不可能的是
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
＞1－
．
