
(本題滿分12分)如圖,在數軸上點A、B、C表示的數分別為-2,1,6,點A與點B之間的距離表示為AB,點B與點C之間的距離表示為BC,點A與點C之間的距離表示為AC.

(1)則AB= ,BC= ,AC= ;
(2)點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和5個單位長度的速度向右運動。請問:BC-AB的值是否隨著運動時間t的變化而改變?若變化,請說明理由;若不變,請求其值;
(3)由第(1)小題可以發現,AB+BC=AC.若點C以每秒3個單位長度的速度向左運動,同時,點A和點B分別以每秒1個單位長度和每秒2個單位長度的速度向右運動.請問:隨著運動時間t的變化, AB、BC、AC之間是否存在類似于(1)的數量關系?請說明理由.
(1)AB= 3 ,BC= 5 ,AC= 8 .
(2)BC-AB的值不會隨著時間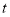 的變化而改變.
的變化而改變.
BC-AB=(5t-2t+5)-(t+2t+3)=2 ;
(3)存在,
AB=t+3
BC=5-5t(t≤1時) 或 BC=5t-5 (t>1時)
AC=8-4t (t≤2時) 或 AC=4t-8(t>2)
當t≤1時,AB+BC=(t+3)+(5-5t)=8-4t=AC
當1<t≤2時,BC+AC=(5t-5)+(8-4t)=t+3=AB
當t>2時,AB+AC=(t+3)+(4t-8)=5t-5=BC.
【解析】
試題分析:(1)根據數軸上兩點間的距離直接可得線段長度;
要想知道(BC-AB)是否隨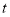 的變化而變化,就要看表示(BC-AB)的代數式是否與t有關,是否含有t.可用含t的代數式把(BC-AB)表示出來再化簡,再作判斷;
的變化而變化,就要看表示(BC-AB)的代數式是否與t有關,是否含有t.可用含t的代數式把(BC-AB)表示出來再化簡,再作判斷;
(3)借助數軸先用t表示AB、BC、AC的長度,AB=t+3;BC=5-5t(t≤1) 或 BC=5t-5 (t>1);AC=8-4t (t≤2時) 或 AC=4t-8(t>2).再根據t的取值來分情況討論.
試題解析:(1)AB= 3 ,BC= 5 ,AC= 8 .
(2)因為A、B兩點是反向運動,所以AB=t+2t+3;因為B、C兩點是同向運動,所以BC=(5t-2t+5).可得BC-AB=(5t-2t+5)-(t+2t+3)=2,即無論t取何值,BC-AB都是2,不會變化;
(3)根據題意可知:
AB=2t+3-t=t+3;
BC=5-2t-3t= 5-5t(t≤1時) 或 BC=2t+3t-5=5t-5 (t>1時);
AC=8-t-3t=8-4t (t≤2時) 或 AC=t+3t-8=4t-8(t>2).
當t≤1時,AB+BC=(t+3)+(5-5t)=8-4t=AC;
當1<t≤2時,BC+AC=(5t-5)+(8-4t)=t+3=AB;
當t>2時,AB+AC=(t+3)+(4t-8)=5t-5=BC.
所以,隨著運動時間t的變化, AB、BC、AC之間存在類似于(1)的數量關系.
考點:(1)數軸上兩點間的距離;(2)用代數式表示數量關系;(3)整式的加減.
考點分析: 考點1:有理數 1、有理數的概念:正數和分數統稱為有理數.

科目:初中數學 來源:2014-2015學年江蘇省七年級上學期第一次質檢數學試卷(解析版) 題型:選擇題
下列各數中:+3、3、-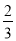 、9、
、9、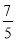 、-(-8)、0、-|+3|,負有理數有( )
、-(-8)、0、-|+3|,負有理數有( )
A.2個 B.3個 C.4個 D.5個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省無錫市錫山區七年級上學期期中考試數學試卷(解析版) 題型:選擇題
如果一個長方形的周長為10,其中長為a,那么該長方形的面積為( )
A.10a B.5 a-a2 C.5a D.10a-a2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省泰州市海陵區七年級上學期中質量調研數學試卷(解析版) 題型:填空題
小麗從出版社郵購5本同樣的書,包括郵費的總價為81元,郵費6元.設每本書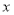 元,可得方程 .
元,可得方程 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山西農業大學附屬中學九年級上學期期末考試數學試卷(解析版) 題型:選擇題
拋物線 的頂點坐標是( )
的頂點坐標是( )
A、(2,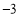 ) B、(
) B、(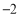 ,3) C、(2,3) D、(
,3) C、(2,3) D、(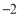 ,
,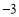 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com