Question

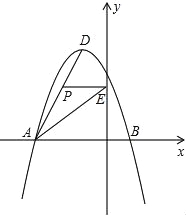
【題目】如圖所示，在平面直角坐標系中，拋物線y=ax2+bx+c經過A（﹣3，0）、B（1，0）、C（0，3）三點，其頂點為D，連接AD，點P是線段AD上一個動點（不與A、D重合），過點P作y軸的垂線，垂足點為E，連接AE．

（1）求拋物線的函數解析式，并寫出頂點D的坐標；

（2）如果P點的坐標為（x，y），△PAE的面積為S，求S與x之間的函數關系式，直接寫出自變量x的取值范圍，并求出S的最大值；

（3）在（2）的條件下，當S取到最大值時，過點P作x軸的垂線，垂足為F，連接EF，把△PEF沿直線EF折疊，點P的對應點為點P′，求出P′的坐標，并判斷P′是否在該拋物線上．

Answer 1

【答案】(1)、y=﹣x2﹣2x+3；D(-1，4)；(2)、S﹣x2﹣3x（﹣3＜x＜﹣1），當x=﹣時，S取最大值；(3)、∴P′（，），不在拋物線上

【解析】

試題分析：(1)、由拋物線y=ax2+bx+c經過A（﹣3，0）、B（1，0）、C（0，3）三點，則代入求得a，b，c，進而得解析式與頂點D．(2)、由P在AD上，則可求AD解析式表示P點．由S△APE=PEyP，所以S可表示，進而由函數最值性質易得S最值．(3)、由最值時，P為（﹣，3），則E與C重合．畫示意圖，P'過作P'M⊥y軸，設邊長通過解直角三角形可求各邊長度，進而得P'坐標．判斷P′是否在該拋物線上，將xP'坐標代入解析式，判斷是否為yP'即可．

試題解析：(1)、∵拋物線y=ax2+bx+c經過A（﹣3，0）、B（1，0）、C（0，3）三點，

∴， 解得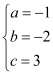：， ∴解析式為y=﹣x2﹣2x+3

∵﹣x2﹣2x+3=﹣（x+1）2+4， ∴拋物線頂點坐標D為（﹣1，4）．

(2)、∵A（﹣3，0），D（﹣1，4）， ∴設AD為解析式為y=kx+b，有， 解得，

∴AD解析式：y=2x+6， ∵P在AD上， ∴P（x，2x+6），

∴S△APE=PEyP=（﹣x）（2x+6）=﹣x2﹣3x（﹣3＜x＜﹣1），當x=﹣時，S取最大值．

(3)、如圖1，設P′F與y軸交于點N，過P′作P′M⊥y軸于點M，

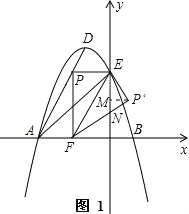
∵△PEF沿EF翻折得△P′EF，且P（﹣，3）， ∴∠PFE=∠P′FE，PF=P′F=3，PE=P′E=，

∵PF∥y軸， ∴∠PFE=∠FEN， ∵∠PFE=∠P′FE， ∴∠FEN=∠P′FE， span>∴EN=FN，

設EN=m，則FN=m，P′N=3﹣m． 在Rt△P′EN中， ∵（3﹣m）2+（）2=m2， ∴m=．

∵S△P′EN=P′NP′E=ENP′M， ∴P′M=． 在Rt△EMP′中

∵EM=， ∴OM=EO﹣EM=， ∴P′（，）．

當x=時，y=﹣（）2﹣2+3=0.39≠， ∴點P′不在該拋物線上．