
【題目】如圖,點A,B的坐標分別為(1,4)和(4,4),拋物線y=a(x-m)2+n的頂點在線段AB上運動,與x軸交于C、D兩點(C在D的左側),點C的橫坐標最小值為-3,則點D的橫坐標最大值為______.

【答案】8.
【解析】
當拋物線y=a(x-m)2+n的頂點在線段AB的A點上時,點C的橫坐標最小把A的坐標代入即可求出a的值,因為拋物線y=a(x-m)2+n的頂點在線段AB上運動,所以拋物線的a永遠等于-![]() ,根據題意可知當拋物線的頂點運動到B時,D的橫坐標最大,把B的坐標和a的值代入即可求出二次函數的解析式,再求出y=0時x的值即可求出答案.
,根據題意可知當拋物線的頂點運動到B時,D的橫坐標最大,把B的坐標和a的值代入即可求出二次函數的解析式,再求出y=0時x的值即可求出答案.
解:當拋物線y=a(x-m)2+n的頂點在線段AB的A點上時,點C的橫坐標最小,
把A(1,4)代入得:y=a(x-1)2+4,
把C(-3,0)代入得:0=a(-3-1)2+4,
解得:a=-![]() ,
,
即:y=-![]() (x-1)2+4,
(x-1)2+4,
∵拋物線y=a(x-m)2+n的頂點在線段AB上運動,
∴拋物線的a永遠等于-![]() ,
,
當拋物線的頂點運動到B時,D的橫坐標最大,把a=-![]() 和B(4,4)代入y=a(x-m)2+n得:
和B(4,4)代入y=a(x-m)2+n得:
y=-![]() (x-4)2+4,
(x-4)2+4,
當y=0時,0=-![]() (x-4)2+4,
(x-4)2+4,
解得:x1=0,x2=8,
∵C在D的左側,
∴點D的橫坐標最大值是8.
故答案為:8.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:
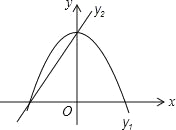
【題目】已知拋物線y1=﹣2x2+2,直線y2=2x+2,當x任取一值時,對應的函數值分別為y1、y2.若y1≠y2,取y1、y2中的較小值記為M;若y1=y2,記M=y1.例如:當x=1時,y1=0,y2=4,y1<y2,此時M=0.下列判斷:①當x>0時,y1>y2;②當x<0時,x值越大,M值越大;③使得M大于2的x值不存在;④使得M=1的x值是﹣![]() 或
或![]() .其中正確結論的個數為( )
.其中正確結論的個數為( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
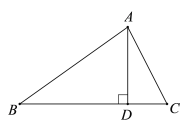
【題目】如圖,△ABC的高為AD.△A'B'C'的高為A'D',且A'D'=AD.現有①②③三個條件:
①∠B=∠B',∠C=∠C';
②∠B=∠B',AB=A'B';
③BC=B'C',AB=A'B'.
分別添加以上三個條件中的一個,如果能判定△ABC≌△A'B'C',寫出序號,并畫圖證明;如果不能判定△ABC≌△A'B'C',寫出序號,并畫出相應的反例圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】大學生小韓在暑假創業,銷售一種進價為![]() 元/件的玩具熊,銷售過程中發現,每周銷售量少(件)與銷售單價
元/件的玩具熊,銷售過程中發現,每周銷售量少(件)與銷售單價![]() (元)之間的關系可近似的看作一次函數:
(元)之間的關系可近似的看作一次函數:![]()
![]() 如果小韓想要每周獲得
如果小韓想要每周獲得![]() 元的利潤,那么銷售單價應定為多少元?
元的利潤,那么銷售單價應定為多少元?
![]() 設小韓每周獲得利潤為
設小韓每周獲得利潤為![]() (元),當銷售單價定為多少元時,每周可獲得利潤最大,最大利潤是多少?
(元),當銷售單價定為多少元時,每周可獲得利潤最大,最大利潤是多少?
![]() 若該玩具熊的銷售單價不得高于
若該玩具熊的銷售單價不得高于![]() 元,如果小韓想要每周獲得的利潤不低于
元,如果小韓想要每周獲得的利潤不低于![]() 元,那么他的銷售單價應定為多少?
元,那么他的銷售單價應定為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代科技的發展已經進入到了5G時代,“5G”即第五代移動通信技術(英語:5th generation mobile networks或5th generation wireless systems、5th-Generation,簡稱5G或5G技術)是最新一代蜂窩移動通信技術,也是即4G(LTE-A、WiMax)、3G(UMTS、LTE)和2G(GSM)系統之后的延伸。中國信息通信科技集團有限公司工程師余少華院士說“同4G相比,5G的傳輸速率提高了10至100倍.”“從人人互聯、人物互聯,到物物互聯,再到人網物三者的結合,5G技術最終將構建起萬物互聯的智能世界” 如果5G網絡峰值速率是4G網絡峰值速率的10倍,那么在峰值速率下傳輸1 000MB數據,5G網絡比4G網絡快90秒,求這兩種網絡的峰值速率(MB/秒).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A表示一個數,若把數A寫成形如 的形式,其中
的形式,其中![]() 、
、![]() 、
、![]() 、
、![]() 、…都為整數.則我們稱把數A寫成連分數形式.
、…都為整數.則我們稱把數A寫成連分數形式.
例如:把2.8寫成連分數形式的過程如下:
2.8-2=0.8,![]() ,
,
1.25-1=0.25,![]() ,
,
4-4=0.

(1)把3.245寫成連分數形式不完整的過程如下:
3.245-3=0.245,![]() ,
,
4.082-4=0.082,![]() ,
,
12.250-12=0.25,![]() ,
,
4-4=0.
∴
則![]() _____________;
_____________;![]() _____________;
_____________;
(2)請把![]() 寫成連分數形式;
寫成連分數形式;
(3)有這樣一個問題:如圖是長為47,寬為10的長方形紙片.從中裁剪出正方形,若長方形紙片無剩余,則剪出的正方形最少是幾個?

小明認為這個問題和 “把一個數化為連分數形式” 有關聯,并把![]() 化成連分數從而解決了問題.你可以參考小明的思路解決上述問題,請直接寫出“剪出的正方形最少”時,正方形的個數.
化成連分數從而解決了問題.你可以參考小明的思路解決上述問題,請直接寫出“剪出的正方形最少”時,正方形的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,張老師舉了下面的例題:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度數.(答案:
的度數.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度數.(答案:
的度數.(答案:![]() 或
或![]() 或
或![]() )
)
張老師啟發同學們進行變式,小敏編了如下兩題:
變式1: 等腰三角形![]() 中,∠A=100°,求
中,∠A=100°,求![]() 的度數.
的度數.
變式2: 等腰三角形![]() 中,∠A= 45° ,求
中,∠A= 45° ,求![]() 的度數.
的度數.
(1)請你解答以上兩道變式題.
(2)解(1)后,小敏發現,![]() 的度數不同,得到
的度數不同,得到![]() 的度數的個數也可能不同.如果在等腰三角形
的度數的個數也可能不同.如果在等腰三角形![]() 中,設
中,設![]() ,當
,當![]() 只有一個度數時,請你探索
只有一個度數時,請你探索![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校部分團員參加社會公益活動,準備購進一批許愿瓶進行銷售,并將所得利潤捐給慈善機構.這種許愿瓶的進價為![]() 元/個,根據市場調查,一段時間內的銷售量
元/個,根據市場調查,一段時間內的銷售量![]() (個)與銷售單價
(個)與銷售單價![]() (元/個)之間的對應關系如圖所示:
(元/個)之間的對應關系如圖所示:

![]() 試判斷
試判斷![]() 與
與![]() 之間的函數關系,并求出函數關系式;
之間的函數關系,并求出函數關系式;
![]() 按照上述市場調查的銷售規律,當利潤達到
按照上述市場調查的銷售規律,當利潤達到![]() 元時,請求出許愿瓶的銷售單價
元時,請求出許愿瓶的銷售單價![]() ;
;
![]() 請寫出銷售利潤
請寫出銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元/個)之間的函數關系式;若許愿瓶的進貨成本不超過
(元/個)之間的函數關系式;若許愿瓶的進貨成本不超過![]() 元,要想獲得最大的利潤,試確定這種許愿瓶的銷售單價,并求出此時的最大利潤.
元,要想獲得最大的利潤,試確定這種許愿瓶的銷售單價,并求出此時的最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com