
【題目】已知點A(﹣1,2)、B(3,6)在拋物線y=ax2+bx上
(1)求拋物線的解析式;
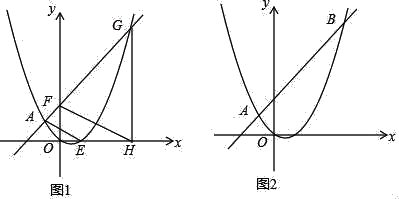
(2)如圖1,點F的坐標(biāo)為(0,m)(m>2),直線AF交拋物線于另一點G,過點G作x軸的垂線,垂足為H.設(shè)拋物線與x軸的正半軸交于點E,連接FH、AE,求證:FH∥AE;
(3)如圖2,直線AB分別交x軸、y軸于C、D兩點.點P從點C出發(fā),沿射線CD方向勻速運(yùn)動,速度為每秒![]() 個單位長度;同時點Q從原點O出發(fā),沿x軸正方向勻速運(yùn)動,速度為每秒1個單位長度.點M是直線PQ與拋物線的一個交點,當(dāng)運(yùn)動到t秒時,QM=2PM,直接寫出t的值.
個單位長度;同時點Q從原點O出發(fā),沿x軸正方向勻速運(yùn)動,速度為每秒1個單位長度.點M是直線PQ與拋物線的一個交點,當(dāng)運(yùn)動到t秒時,QM=2PM,直接寫出t的值.
【答案】(1)拋物線的解析式為y=x2﹣x;(2)證明見解析;(3)當(dāng)運(yùn)動時間為![]() 或
或![]() 秒時,QM=2PM.
秒時,QM=2PM.
【解析】
(1)(1)A,B的坐標(biāo)代入拋物線y=ax2+bx中確定解析式;
(2)把A點坐標(biāo)代入所設(shè)的AF的解析式,與拋物線的解析式構(gòu)成方程組,解得G點坐標(biāo),再通過證明三角形相似,得到同位角相等,兩直線平行;
(3)具體見詳解.
.解:(1)將點A(﹣1,2)、B(3,6)代入中,
![]() ,解得:
,解得:![]() ,
,
∴拋物線的解析式為y=x2﹣x.
(2)證明:設(shè)直線AF的解析式為y=kx+m,
將點A(﹣1,2)代入y=kx+m中,即﹣k+m=2,
∴k=m﹣2,
∴直線AF的解析式為y=(m﹣2)x+m.
聯(lián)立直線AF和拋物線解析式成方程組,
![]() ,解得:
,解得:![]() 或
或![]() ,
,
∴點G的坐標(biāo)為(m,m2﹣m).
∵GH⊥x軸,
∴點H的坐標(biāo)為(m,0).
∵拋物線的解析式為y=x2﹣x=x(x﹣1),
∴點E的坐標(biāo)為(1,0).
過點A作AA′⊥x軸,垂足為點A′,如圖1所示.
∵點A(﹣1,2),
∴A′(﹣1,0),
∴AE=2,AA′=2.
∴![]() =1,
=1,![]() =
=![]() =1,
=1,
∴![]() =
= ![]() ,
,
∵∠AA′E=∠FOH,
∴△AA′E∽△FOH,
∴∠AEA′=∠FHO,
∴FH∥AE.
(3)設(shè)直線AB的解析式為y=k0x+b0,
將A(﹣1,2)、B(3,6)代入y=k0x+b0中,得 ![]() ,解得:
,解得:![]() ,
,
∴直線AB的解析式為y=x+3,
當(dāng)運(yùn)動時間為t秒時,點P的坐標(biāo)為(t﹣3,t),點Q的坐標(biāo)為(t,0).
當(dāng)點M在線段PQ上時,過點P作PP′⊥x軸于點P′,過點M作MM′⊥x軸于點M′,則△PQP′∽△MQM′,如圖2所示,
∵QM=2PM,
∴![]() =
=![]() ,
,
∴QM′=![]() QP'=2,MM′=
QP'=2,MM′=![]() PP'=
PP'=![]() t,
t,
∴點M的坐標(biāo)為(t﹣2,![]() t).
t).
又∵點M在拋物線y=x2﹣x上,
∴![]() t=(t﹣2)2﹣(t﹣2),
t=(t﹣2)2﹣(t﹣2),
解得:t=![]() ;
;
當(dāng)點M在線段QP的延長線上時,
同理可得出點M的坐標(biāo)為(t﹣6,2t),
∵點M在拋物線y=x2﹣x上,
∴2t=(t﹣6)2﹣(t﹣6),
解得:t=![]() .
.
綜上所述:當(dāng)運(yùn)動時間秒![]() 或
或![]() 時,QM=2PM.
時,QM=2PM.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某文化用品商店用2000元購進(jìn)一批學(xué)生書包,面市后發(fā)現(xiàn)供不應(yīng)求,商店又購進(jìn)第二批同樣的書包,所購數(shù)量是第一批購進(jìn)數(shù)量的3倍,但單價貴了4元,結(jié)果第二批用了6300元。
(1)求第一批購進(jìn)書包的單價是多少元?
(2)若商店銷售這兩批書包時,每個售價都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,二次函數(shù)y=ax2+bx+c(a≠0)的圖象經(jīng)過點(﹣1,2),且與x軸交點的橫坐標(biāo)為x1、x2,其中﹣2<x1<﹣1、0<x2<1下列結(jié)論:①4a﹣2b+c<0②2a﹣b<0③abc>0④b2+8a>4ac正確的結(jié)論是_____.
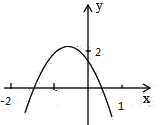
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,點D在線段AC上,且CD=7cm,動點P從距B點15cm的E點出發(fā),以每秒2cm的速度沿射線EA的方向運(yùn)動,時間為t秒.
(1)求AD的長.
(2)用含有t的代數(shù)式表示AP的長.
(3)在運(yùn)動過程中,是否存在某個時刻,使△ABC與△ADP全等?若存在,請求出t值;若不存在,請說明理由.
(4)直接寫出t=______秒時,△PBC為等腰三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
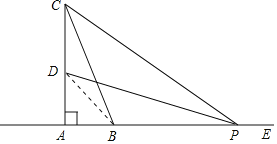
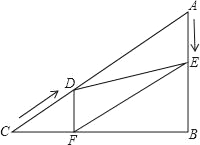
【題目】如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發(fā)沿CA方向以4cm/s的速度向點A勻速運(yùn)動,同時點E從點A出發(fā)沿AB方向以2cm/s的速度向點B勻速運(yùn)動,當(dāng)其中一個點到達(dá)終點時,另一個點也隨之停止運(yùn)動.設(shè)點D,E運(yùn)動的時間是ts(0<t≤15).過點D作DF⊥BC于點F,連接DE,EF.
(1)求證:四邊形AEFD是平行四邊形;
(2)當(dāng)t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
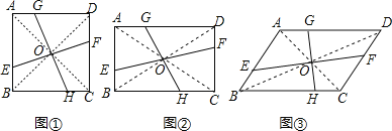
【題目】在四邊形ABCD中,對角線AC、BD相交于點O,過點O的直線分別交邊AB、CD、AD、BC于點E、F、G、H
(感知)如圖①,若四邊形ABCD是正方形,且EF⊥GH,易知S△BOE=S△AOG,又因為S△AOB=![]() S四邊形ABCD,所以S四邊形AEOG=
S四邊形ABCD,所以S四邊形AEOG=![]() S正方形ABCD(不要求證明);
S正方形ABCD(不要求證明);
(拓展)如圖②,若四邊形ABCD是矩形,且S四邊形AEOG=![]() S矩形ABCD,若AB=a,AD=b,BE=m,求AG的長(用含a、b、m的代數(shù)式表示);
S矩形ABCD,若AB=a,AD=b,BE=m,求AG的長(用含a、b、m的代數(shù)式表示);
(探究)如圖③,若四邊形ABCD是平行四邊形,且S四邊形AEOG=![]() SABCD,若AB=3,AD=5,BE=1,則AG=______.
SABCD,若AB=3,AD=5,BE=1,則AG=______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小敏思考解決如下問題:
原題:如圖1,四邊形ABCD中![]() ,
,![]() ,
,![]() 點P,Q分別在四邊形ABCD的邊BC,CD上,
點P,Q分別在四邊形ABCD的邊BC,CD上,![]() ,求證:
,求證:![]() .
.
![]() ______;
______;
![]() 小敏進(jìn)行探索,如圖2,將點P,Q的位置特殊化,使
小敏進(jìn)行探索,如圖2,將點P,Q的位置特殊化,使![]() ,
,![]() ,點E,F分別在邊BC,CD上,此時她證明了
,點E,F分別在邊BC,CD上,此時她證明了![]() 請你證明此時結(jié)論;
請你證明此時結(jié)論;
![]() 受以上
受以上![]() 的啟發(fā),在原題中,添加輔助線:如圖3,作
的啟發(fā),在原題中,添加輔助線:如圖3,作![]() ,
,![]() ,垂足分別為E,F,請你繼續(xù)完成原題的證明.
,垂足分別為E,F,請你繼續(xù)完成原題的證明.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com